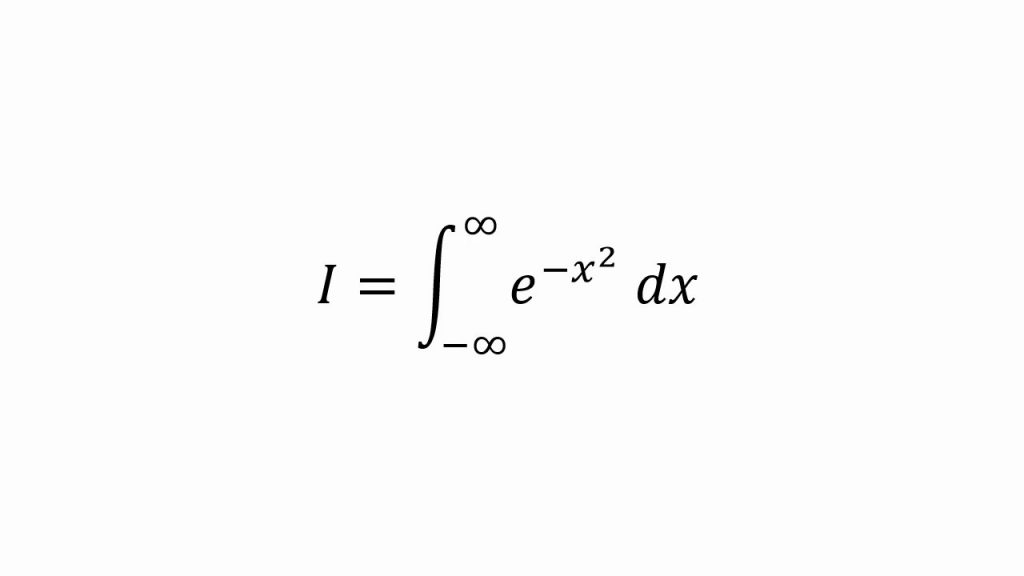
La integral de Gauss
En esta entrada vamos a calcular el valor de la integral impropia de la función gaussiana \(e^{-x^{2}}\) sobre todo el dominio de x entre \(-\infty \ y \ \infty\). Es decir, la integral de Gauss.
Es una integral muy peculiar e importante. Por un lado, esta integral tiene amplias aplicaciones, incluyendo la normalización, la teoría de la probabilidad y la transformada continua de Fourier.
Por otro, no existe una primitiva como tal para \(\int e^{-x^{2}} dx\). Sin embargo, empleando un procedimiento muy curioso, podemos calcular el valor de dicha integral extendida a todo el dominio de x.
El método de resolución
En principio no podemos calcular directamente la integral, por lo que en un primer paso calculamos su valor al cuadrado.
\(I= \int_{-\infty}^{\infty} e^{-x^{2}} dx\) \(I^{2}= \int_{-\infty}^{\infty} e^{-x^{2}} dx \ * \ \int_{-\infty}^{\infty} e^{-x^{2}} dx \)¿Bien? Ahora, en vez de considerar 2 veces la variable x, una de las integrales la integramos respecto a y, extendiendo la integral al recinto de \(R^{2}\) convirtiéndola en una integral doble.
\(I^{2}= \int_{-\infty}^{\infty} e^{-x^{2}} dx \ * \ \int_{-\infty}^{\infty} e^{-y^{2}} dy=\) \(= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-x^{2}}* e^{-y^{2}} dxdy= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-(x^{2}+ y^{2})} dxdy \)¿Sigues estando de acuerdo? Ahora llega el truco. Estamos integrando en todo el recinto de \(R^{2}\) que, en coordenadas polares, equivale a integrar con \(\ \theta \ entre \ 0 \ y \ 2\pi\) y con \(r \ entre \ 0 \ y \ \infty\).
Vamos a realizar un cambio de variable a polares, y eso supone multiplicar por el jacobiano r. Además, sabemos que \(x^{2}+y^{2}=r^{2}\).
\(I^{2}= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-(x^{2}+ y^{2})} dxdy = \) \(= \int_{0}^{\infty} \int_{0}^{2\pi} r*e^{-r^{2}} d\theta dr =2\pi \int_{0}^{\infty} r*e^{-r^{2}} dr \)Y sabiendo que \(\int r*e^{-r^{2}} dr= -\frac{1}{2}e^{-r^{2}} + C\)
\(I^{2}=2\pi * [-\frac{1}{2}e^{-r^{2}}]_{0}^{\infty}=\pi * [-\frac{1}{e^{\infty}} + e^{0}]=\pi\)Llegando finalmente a \(I=\sqrt{\pi}\), por lo que se tiene que la integral de Gauss es:
\( \int _{-\infty }^{\infty }e^{-x^{2}}\,dx={\sqrt {\pi }} \)


Y TU DEJA REFERENCIAS NO SEAS COPIONASO
¿Qué referencia quieres que deje amigo? La clase de Matemáticas III que recibí en la facultad? En este artículo no hay ninguna información más allá que la de un uso correcto de las reglas de integración y el cambio de variable.
Un saludo
Muchas gracias, no deje de subir estas explicaciones. No es necesario bibliografía, toodos sabemos que mayoritariamente es Stewart.
Buen resumen. Y sí, ciertamente es material de un segundo o tercer curso de matemáticas y si alguien quiere profundizar un poco más la información se puede encontrar en cualquier sitio, que esto son cosas de hace dos siglos y no es precisamente materia protegida ni puntera. No sé a qué viene el comentario del tal Pajares.
Muchas gracias Oscar!!!