
El 24 de Mayo del año 2000 el Clay Mathematics Institute planteó 7 problemas matemáticos de gran complejidad. Son problemas clásicos que se han resistido a los matemáticos durante años. A estos se les conoce como los problemas del milenio.
El premio por hallar la solución de cualquiera de los problemas es de un millón de dolares. Numerosos catedráticos, científicos, investigadores… han dedicado su carrera al estudio de alguno de los problemas sin éxito alguno.
A día de hoy, casi 20 años después, sólo 1 de los problemas del milenio ha sido resuelto.
P versus NP
El problema «P versus NP» es un problema del milenio del ámbito de la ciencia de la computación.
Cuando queremos calcular la solución a un problema matemático propuesto, debemos de elaborar un algoritmo o una serie de pasos a seguir para resolver cualquier problema del tipo que queremos resolver. Ejemplos de problemas son: Ordenar una tira de números de menor a mayor, calcular todos los factores de un número, calcular el número de combinaciones ganadores de la lotería…
Por ejemplo, para ordenar números hay diferentes algoritmos, unos mejores que otros. El hecho de que haya varios es porque no hay uno que sea el mejor. Un algoritmo muy simple que consista en recorrer todos los números mientras se ordenan (burbuja o selection) es más estable porque da igual cómo de mal ordenados estén inicialmente los números que se tarda «lo mismo». Un algoritmo más complejo que consista por ejemplo en dividir los números en grupos cada vez más pequeños y ordenándolos entre sí es más inestable porque cuanto más dispares sean los grupos más tiempo se empleará en ordenarlos.
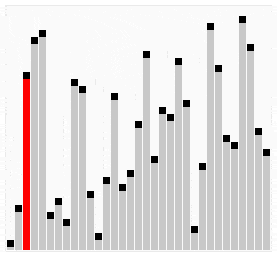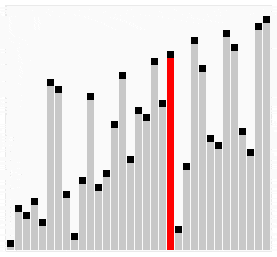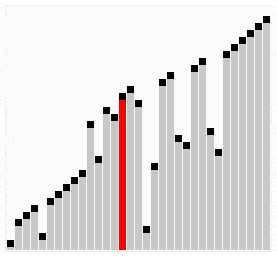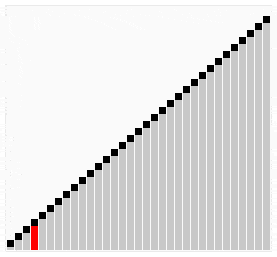
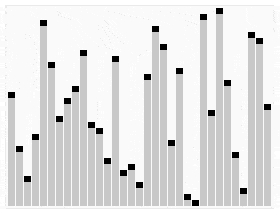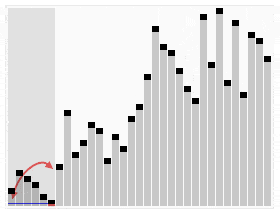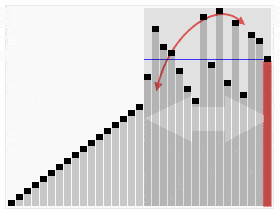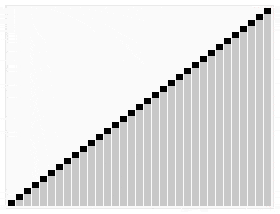
En el ámbito de la informática para cada problema se establece un «orden de complejidad«, que indica la «dificultad» o aumento del tiempo de computación a medida que aumenta el problema. Existe complejidad constante, lineal, cuadrática, exponencial…
Un ejemplo de problema de complejidad constante es hacer una suma. Da igual el tamaño de los números ya que la operación es única. El producto de números o el cálculo de potencias son de orden más complejo.
Un problema P (Polinómico) se caracteriza porque su solución puede hallarse en «tiempo polinómico». Esto es un tiempo razonable de resolución. Además, si una solución puede hallarse en un tiempo razonable, también puede comprobarse si una solución es válida relativamente rápido.
Un problema NP (No polinómico) es un problema cuyo tiempo de resolución es muy elevado. Sin embargo, si logramos hallar una solución, podemos comprobar relativamente rápido si es una solución válida para nuestro problema.
Un ejemplo de problema NP es el Sudoku. Dado un tablero con las casillas parcialmente vacías, hallar la solución supone plantear y resolver un sistema de ecuaciones bastante denso. Además, si aumentásemos las casillas (Imaginemos, aunque no es coherente con las reglas del Sudoku, un Sudoku de 90×90) tardaríamos muchísimo tiempo en calcular la solución.
Sin embargo, comprobar si una solución es válida es relativamente sencillo, ya que consistiría en comprobar que no hay números repetidos en las n filas.
El problema P versus NP aspira a demostrar que o P=NP o que P≠NP. Es decir, demostrar que los problemas fáciles de comprobar son también fáciles de resolver, o que hay problemas que son difíciles de resolver pero fáciles de comprobar. Lo verdaderamente interesante sería que P=NP ya que supondría una revolución en la computación.
La lógica nos llega a pensar que P≠NP. No obstante, no está demostrado. Y esto sucede porque las matemáticas no son capaces de distinguirlos. Definimos la complejidad de un problema como lo óptimo que sea el mejor algoritmo para dicho problema. Y constantemente surgen mejores algoritmos que mejoran la resolución de algunos problemas, no estando fijada la dificultad.
La conjetura de Poincaré
En topología, el homeomorfismo establece una relación de semejanza entre diferentes figuras. Se dicen que dos figuras son homeomorfas si son idénticas a efectos de sus propiedades / características, de manera que deformando, estirando y doblando podemos obtener diferentes formas. Un ejemplo de homeomorfismo es lo que hice sin darme cuenta en el artículo Cómo salir de un laberinto deformando la superficie interior del laberinto como 2 rectas. A efectos de propiedades son idénticos, y es por ello que pude demostrar que el método de la mano derecha es válido, ya que pude acceder a una forma mucho más sencilla e intuitiva.

Una variedad es una generalización del concepto de curva y superficie en espacios de mayor dimensión. Una curva en el plano \(R^{2}\) es una 1-variedad. Una superficie en \(R^{3}\) es una 2-variedad. De esta forma, la esfera que conocemos como tal sería una 2-variedad, siendo denominada 2-esfera. Una 3-variedad es un objeto de \(R^{4}\) (4 dimensiones), y un ejemplo claro es la 3-esfera.
Un recinto compacto es un recinto cerrado y acotado. Es decir, finito.
Un recinto simplemente conexo es, básicamente, uno que no tenga agujeros. La 2-esfera lo es pero el toroide no. Se puede saber si un recinto lo es si somos capaces de, teniendo una cinta rodeando la superficie, comenzar a reducirla hasta obtener un punto.

La conjetura de Poincaré dice lo siguiente:
Toda 3-variedad compacta y simplemente conexa es homeomorfa a la 3-esfera
Aunque el enunciado general es:
Toda n-variedad compacta y simplemente conexa es homeomorfa a la n-esfera
Se demuestra fácilmente para n=1 y n=2. Además, se demostró para n>6, n=6, n=5 y n=4. Sin embargo el caso de n=3 se resistió durante años y, si bien Poincaré lo predijo, no lo pudo demostrar y por eso se quedó en conjetura.
Así, la esfera es una 2-variedad cerrada y simplemente conexa y se estableció que toda variedad de dimensión 2, cerrada y simplemente conexa es homeomorfa a la esfera. Dicho de otro modo: sólo hay una variedad (homeomórfica) de dimensión n=2, cerrada y simplemente conexa, y se trata de la esfera (y sus homeomorfos).
Del mismo modo y tras haber sido demostrado matemáticamente, podemos decir que topológicamente hablando sólo hay una 3-variedad compacta y simplemente conexa: la 3-esfera. Se tiene que cualquier otra 3-variedad compacta y simplemente conexa es homeomorfa a ella. Este es el único de los problemas del milenio demostrado hasta la fecha.
Grigori Perelman
Grigori Perelman es un matemático ruso que ha hecho contribuciones a la topología geométrica. Además, consiguió resolver la conjetura de Poincaré, el único problema del milenio que ha sido resuelto.
Tras graduarse, Perelman dedicó su carrera a la investigación. En 1996 se puso a trabajar sólo en la conjetura de Poincaré (4 años antes de que se publicaran los problemas del milenio).

Entre los años 2002 y 2003, Perelman, tras negarse a compartir la información con revistas privadas, publicó tres de sus famosos artículos en Internet. En ellos describió brevemente el método original para probar la conjetura de Poincaré. Además dio conferencias y tuvo reuniones con otros matemáticos explicando el procedimiento.
Inmediatamente después a la aparición de dicha información, varios grupos de matemáticos se comprometieron a verificar los resultados de Perelman para hacerlo oficial. Sin embargo, un grupo de matemáticos chinos intentaron el plagio, afirmando haber realizado investigaciones inéditas que completaban realmente la resolución del problema. No obstante fueron desacreditados posteriormente.
En el año 2006 decidieron darle a Perelman la medalla Fields, el mayor premio del ámbito de las matemáticas y análogo a los premios Nobel.
El presidente de la Unión Matemática Internacional estuvo intentando convencer a Perelman durante dos días de que la aceptara hasta que se rindió. Dos semanas más tarde Perelman resumió la conversación de este modo:
Él me propuso tres alternativas: acepta y ven; acepta y no vengas, y te enviaremos la medalla luego; tercero, no aceptes ni vengas. Desde el principio le dije que había escogido la tercera.
El premio era completamente irrelevante para mí. Todo el mundo entiende que, si la demostración es correcta, entonces no se necesita ningún otro reconocimiento .
En el año 2010 Perelman ganó el premio del milenio por resolver el problema, pero también lo rechazó.
A día de hoy vive retirado del mundo de las matemáticas, desempleado y viviendo con su madre. No está decepcionado con las matemáticas, sino más bien inmerso en la idea galileana de que:
El humilde razonamiento de uno vale más que la autoridad de miles
No quiere convertirse en ninguna persona conocida ni ser ningún símbolo o «mascota» de nada. Tampoco quiere el dinero ya que lo único que le importa es demostrar teoremas y aumentar el conocimiento matemático.
De alguna manera, el intento de plagio por parte de los chinos le había afectado al darse cuenta de cómo ciertos sectores del ámbito de las matemáticas estaban ahí no por aumentar el conocimiento matemático, sino por el reconocimiento propio.
La conjetura de Hodge
La conjetura de Hodge es un enunciado matemático que se basa en la estructura de ciertos tipos de espacios geométricos conocidos como variedades algebraicas. Fue propuesta por primera vez por el matemático W. V. D. Hodge en la década de 1950 y desde entonces ha sido uno de los principales focos de investigación en geometría algebraica.
Una variedad algebraica es un espacio geométrico que puede describirse mediante un conjunto de ecuaciones polinómicas. Por ejemplo, el círculo \(x^{2} + y^{2} = 1\) es una variedad algebraica, ya que puede describirse mediante la ecuación \(f(x,y) = x^{2} + y^{2} – 1 = 0\). Las variedades algebraicas pueden ser bastante complejas y tener muchas formas diferentes, desde curvas sencillas como círculos y elipses hasta superficies más complicadas como toroides y esferas.
La conjetura de Hodge es una afirmación sobre la estructura de estas variedades algebraicas y cómo pueden descomponerse en piezas más sencillas. En concreto, se refiere al concepto de descomposición de Hodge, que es una forma de expresar una variedad algebraica como una suma de subespacios más sencillos llamados ciclos de Hodge.
La conjetura afirma que cualquier ciclo de Hodge en una variedad algebraica puede representarse como una combinación de ciclos algebraicos, que son subespacios definidos por ecuaciones polinómicas. En otras palabras, la Conjetura de Hodge afirma que todo ciclo de Hodge puede construirse a partir de ciclos algebraicos más sencillos mediante un proceso llamado «reducción algebraica».
La Conjetura de Hodge tiene importantes implicaciones para el estudio de la geometría algebraica y ha atraído la atención de muchos matemáticos a lo largo de los años. Sin embargo, a pesar de los grandes progresos realizados, sigue sin resolverse y se considera uno de los problemas más difíciles de las matemáticas.
Una de las principales razones por las que la conjetura de Hodge es tan difícil de demostrar es que implica un profundo conocimiento de la estructura geométrica y topológica de las variedades algebraicas. Requiere una síntesis de varias técnicas e ideas matemáticas, incluyendo álgebra, geometría y topología, y exige un alto nivel de abstracción y creatividad para resolverla.
A pesar de la dificultad de la conjetura, se ha avanzado mucho hacia su resolución. Muchos matemáticos notables, entre ellos el ya mencionado Grigori Perelman, han contribuido significativamente a la comprensión de la Conjetura de Hodge y han realizado importantes avances en el campo de la geometría algebraica.
La hipótesis de Riemann
La hipótesis de Riemann puede ser considerada como el problema más importante de los 7 problemas del milenio planteados. E incluso de las matemáticas actuales. Lleva sin ser resuelto 160 años y es el único problema del milenio que también pertenece a otra lista de problemas importantes: Los problemas de Hilbert.
La hipótesis se centra alrededor de los números primos, los cuales han intentado ser predichos por los matemáticos desde tiempos inmemorables.
Hay numerosos algoritmos para tratar de predecir números primos. Uno de los más conocidos es la «Criba de Eratóstenes» que permite hallar los números primos menores a un número natural n dado. Para más información entra aquí
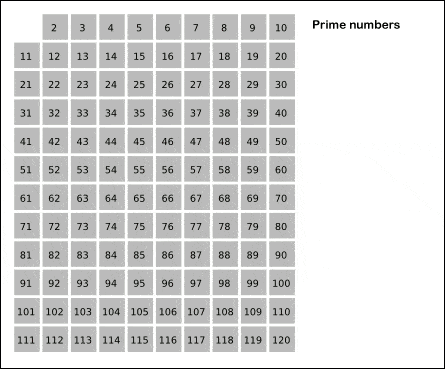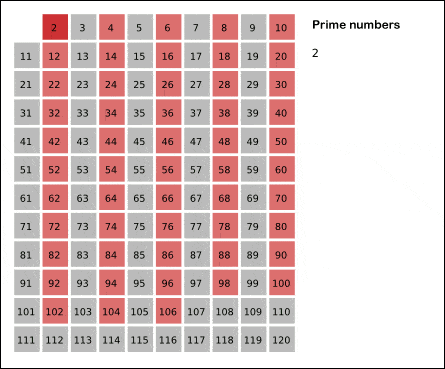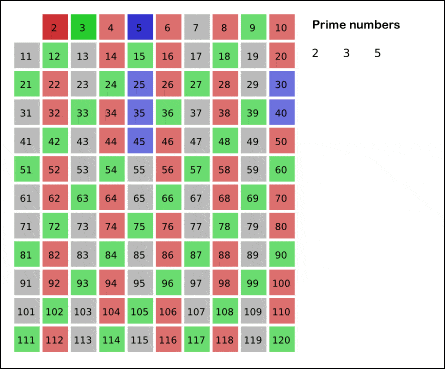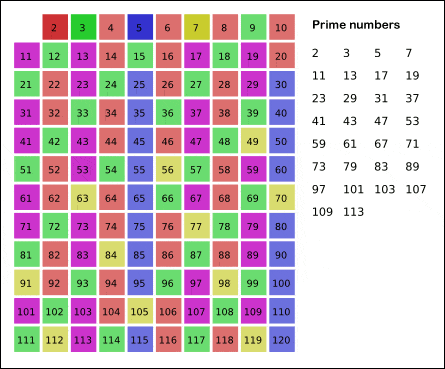
Este tipo de métodos demuestran que, a medida que aumenta el orden de los números, encontramos menos primos. Si bien entre el 1 y el 1000 hay 168 primos, entre el 100.000 y el 101.000 hay sólo 81. Si buscamos los primos entre \(10^{100}\) y \(10^{100}+1000\) vemos que sólo hay 2. Esto da a pensar que se trata de un comportamiento asintótico. Es por ello que el estudio airtmético pasa a ser un estudio analítico empleando conceptos de funciones y límites.
Aparece la función \(\pi(x)\), la cual indica la cantidad de números primos menores o iguales que x. Esta función no tiene una forma definida aunque, Gauss, tras estudiar su comportamiento establece que para números grandes, \(\pi(x) \approx \frac{x}{ln(x)}\)
Es decir; \(\lim_{x \to \infty} \frac{\pi(x)}{ (\frac{x}{ln(x)} )}= 1\)
Ahí no quedó la cosa, ya que Dirichlet encontró una forma de aproximación más precisa a \(\pi(x)\), que denominó como el logaritmo integral Li(x)
\(Li(x)=\int_{0}^{x}\frac{dt}{ln(t)}\)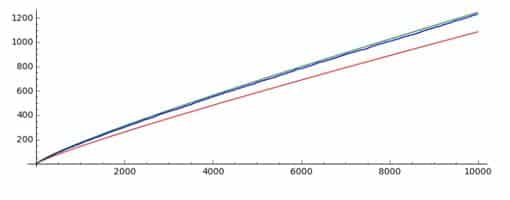
Vamos a dejar a un lado por un momento la distribución de números primos.
En 1737 Leonhard Euler describió una función como una serie numérica de suma de fracciones a la que llamó función Zeta ζ(x):
\(\zeta (x) = \sum_{n=1}^{\infty} \frac{1}{n^{x}} = 1+ \frac{1}{2^{x}} + \frac{1}{3^{x}} + \frac{1}{4^{x}} + \frac{1}{5^{x}} + \cdots (x>1)\)Que es convergente para valores de x estrictamente mayor a 1. De esta función aparecen valores notables como el concepto de serie armónica con x=1 , el problema de Basilea para x=2 obteniendo \(\frac{\pi^{2}}{6}\) o la constante de Apéry con x=3. Euler se basó en ella para enunciar lo que se conoce como el Producto de Euler:
\( \quad \sum _{n=1}^{\infty }\,{\frac {1}{n^{s}}}=\prod _{p}{\frac {1}{1-p^{-s}}} \)Siendo p cada uno de los números primos. De esta manera demostró que existe una cantidad infinita de números primos. La demostración se encuentra aquí
Riemann se dio cuenta del potencial de dicha función y decidió extender su estudio al de los números complejos. Los denotaremos como s=a+bi. Es así como surge la conocida Función Zeta de Riemann ζ(s):
\(\zeta (s) = \sum_{n=1}^{\infty} \frac{1}{n^{s}}= {\frac {1}{1^{s}}}+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+\cdots , con \ Re(s)>1\)Se exige que la parte real sea estrictamente mayor que la unidad para que la función pueda ser convergente en su dominio. De esta función nos interesan dos cosas: Los ceros (Puntos donde la función toma el valor 0) y los polos (Puntos donde la función se hace infinita).
Se sabe que la función tiene ceros «triviales» para los números enteros pares negativos (-2,-4,-6,-8)…
Aparte de los ceros triviales, la función también se anula en valores de s que están dentro del rango {s ∈ C: 0 < Re(s) < 1}, y que son llamados ceros no triviales, debido a que es más difícil demostrar la ubicación de esos ceros dentro del rango crítico.
Y aquí es donde llega el enunciado del problema:
La hipótesis de Riemann asegura que cualquier cero no trivial tiene que cumplir Re(s)=1/2, por lo tanto, todos los ceros están alineados en el plano complejo formando una recta, llamada recta crítica.
La localización de estos ceros tiene significativa importancia en teoría de números, ya que, por ejemplo, el hecho de que todos los ceros estén en el rango crítico demuestra el teorema de los números primos.
El teorema de los números primos es un enunciado que describe la distribución asintótica de los números primos. Esto formaliza la idea intuitiva de que los números primos son menos comunes cuanto más grandes son. Es uno de los teoremas más importantes de la historia de las matemáticas por su influencia en el desarrollo posterior de la investigación de los números primos. Esta idea es la que he introducido al principio de la explicación del problema y la consecuencia de demostrar la hipótesis de Riemann.
Yang-Mills y el salto de masa (mass gap)
Uno de los descubrimientos más importantes realizados en la primera parte del siglo pasado fue el comportamiento cuántico del mundo físico.
A distancias muy cortas, como el tamaño de un átomo o inferiores, el mundo se comporta de manera muy diferente al mundo «clásico» al que estamos acostumbrados.
Una de las características más conocidas del mundo cuántico es la llamada dualidad onda-partícula; partículas como los electrones se comportan a veces como si fueran partículas o cuerpos puntuales con una posición definida, y a veces como si fueran ondas.
Este comportamiento no solo tiene interés teórico ya que sustenta gran parte de nuestra tecnología moderna. El conocimiento de esta rama de la física es fundamental para el comportamiento de los semiconductores, de los nanomateriales, la computación cuántica… En definitiva, el futuro.
Hace casi medio siglo, Yang y Mills introdujeron una nueva teoría para describir partículas elementales utilizando estructuras que se basan en la geometría. La teoría cuántica de Yang-Mills es ahora la base de la mayoría de las teorías de partículas elementales, y sus predicciones se han probado en muchos laboratorios experimentales, pero su base matemática aún no está clara.
La teoría de Yang-Mills es una generalización de la teoría unificada del electromagnetismo de James Clerk Maxwell usada para describir la fuerza nuclear débil (Responsable entre otras cosas de la radiación) y fuerte (Permite la unión de protones y neutrones en un núcleo estable) en partículas subatómicas.
El uso de la teoría de Yang-Mills para describir las fuertes interacciones de las partículas elementales depende de una sutil propiedad mecánica cuántica llamada salto de masa o mass gap: las partículas cuánticas tienen masas positivas, aunque las ondas clásicas viajan a la velocidad de la luz.
En la teoría cuántica de campos el salto de masa o mass gap es la diferencia de energia entre el estado de mínima energía (El vacío) y el siguiente estado de mínima energía.
La energía del vacío por definición es cero, y suponiendo que los estados de energía pueden pensarse como partículas en ondas planas, el salto de masa es la masa de la partícula más ligera.
Esta propiedad ha sido descubierta por físicos a partir de experimentos y confirmada por simulaciones en ordenadores, y se cree que es la razón por la cual la fuerza nuclear fuerte solo actúa en distancias muy pequeñas. Pero aún no se ha entendido desde un punto de vista teórico. El progreso en establecer la existencia de la teoría de Yang-Mills y el mass-gap requerirá la introducción de nuevas ideas fundamentales tanto en física como en matemáticas.
Es por ello que, la formalización matemática de esta teoría se propuso como problema del milenio. El enunciado del problema dice así:
Probar que para todo grupo de Lie compacto simple G, la teoría cuántica de Yang–Mills en \(\mathbb{R}^{4} \) existe y tiene un salto de masa ∆ > 0.
El problema es que en la teoría clásica de Yang–Mills las partículas no tienen masa. Sin embargo todos los experimentos, y en particular el fenómeno denominado libertad asintótica, indican que en la teoría cuántica los campos de Yang–Mills que describen las interacciones nucleares tienen masa no nula. El problema propuesto por el Instituto Clay de Matemáticas consiste en demostrar de modo matemáticamente riguroso la existencia de la teoría de Yang–Mills cuántica y la existencia del salto de masa.
Las ecuaciones de Navier-Stokes
Llegamos al problema del milenio más interesante desde un punto de vista ingenieril y altamente relacionado con la aerodinámica y el movimiento de los fluidos: La resolución de las Ecuaciones de Navier-Stokes.
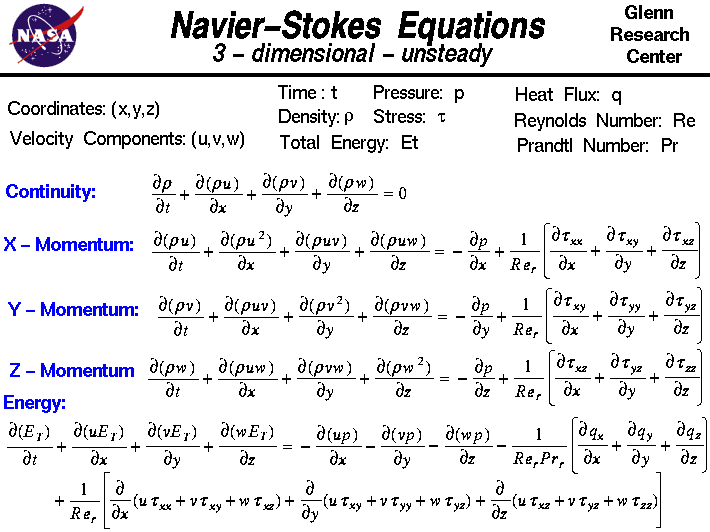
Para definir el movimiento de una partícula puede emplearse la segunda Ley de Newton:
\(\vec{F} = m \cdot \vec{a}\)
De esa forma, conocidas las fuerzas ejercidas sobre la partícula \(\vec{F}\), podemos obtener su aceleración \(\vec{a}\) y tras integrarla en el tiempo obtener su posición \(\vec{r}\).
Para analizar el movimiento de un fluido se parte de una idea similar: consideramos cada una de las pequeñas partículas infinitesimales que componen un fluido (vamos a suponer cada gota) y aplicamos las ecuaciones de la dinámica por medio de la integración del comportamiento de estas partículas en un volumen de control. Extrapolando la ecuación de conservación de la masa al fluido (1), ecuación de conservación de cantidad de movimiento (3), y ecuación de conservación de la energía (1) obtenemos las 5 ecuaciones que componen las Ecuaciones de Navier-Stokes. Tengo un artícula dedicado exclusivamente a su deducción y aplicación:
Sin embargo, el movimiento de un fluido es tan caótico que las ecuaciones adquieren una gran complejidad en su resolución y sólo pueden resolverse numéricamente o analíticamente por medio de muchas simplificaciones e idealizaciones del fluido. Los programas que simulan el movimiento de fluidos (CFD) emplean el método de elementos finitos dividiendo el fluido en pequeñas regiones y aplicando las ecuaciones localmente y con incrementos de tiempo. A mayor número de regiones y menor incremento de tiempo, el error de cálculo acumulado disminuye. Es por ello que para realizar simulaciones precisas se requieren de ordenadores extremadamente potentes y mucho tiempo de cálculo.
La obtención de una solución general de dichas ecuaciones sería una revolución en la historia de la ingeniería porque podría analizarse el movimiento de fluidos con muchísima rapidez y sin error asociado. Esto es precisamente lo que se pide en este problema.
La conjetura de Birch y Swinnerton-Dyer
La conjetura de Birch y Swinnerton-Dyer es un famoso problema matemático sin resolver relacionado con el comportamiento de las curvas elípticas, que son curvas algebraicas que pueden definirse mediante una ecuación de la forma \(y^{2} = x^{3} + a \cdot x + b\). Las curvas elípticas tienen una historia fascinante que se remonta a los trabajos del antiguo matemático griego Diofanto, que las utilizó para estudiar soluciones enteras de ecuaciones. Más recientemente, las curvas elípticas han desempeñado un papel fundamental en el desarrollo de la geometría algebraica moderna y la teoría de números.
La conjetura relaciona las propiedades algebraicas de una curva elíptica con las propiedades analíticas de la curva, concretamente con la distribución de los puntos de la curva que tienen coordenadas racionales. La conjetura afirma que el rango del grupo de puntos racionales de una curva elíptica es igual al orden de desaparición de una determinada función, denominada función L, en un punto concreto. El rango de una curva elíptica es una medida del tamaño del grupo de puntos racionales de la curva, mientras que la función L es una función de valor complejo que codifica información importante sobre la curva.
Una forma de entender la conjetura de Birch y Swinnerton-Dyer es considerar la siguiente analogía: imagínate un mapa de una ciudad, donde las calles representan los puntos racionales de una curva elíptica y las intersecciones representan los puntos algebraicos de la curva. La conjetura afirma que el número de intersecciones (es decir, el rango) está relacionado con el número de calles (es decir, el orden de desaparición de la función L). Esta analogía no es perfecta, pero da una idea de la relación entre los aspectos algebraicos y analíticos de la curva que la conjetura pretende captar.
La conjetura de Birch y Swinnerton-Dyer tiene importantes implicaciones para la teoría de números y la geometría algebraica. Ha sido ampliamente estudiada y ha atraído la atención de muchos matemáticos de primera fila, que han logrado avances significativos en la comprensión de la conjetura y sus conexiones con otras áreas de las matemáticas. En particular, la conjetura se ha relacionado con otros famosos problemas sin resolver, como la Hipótesis de Riemann y el programa Langlands, que trata de comprender las conexiones entre distintas áreas de las matemáticas.
A pesar de los muchos esfuerzos realizados, la conjetura de Birch y Swinnerton-Dyer sigue sin tener una demostración general y se considera uno de los problemas sin resolver más importantes de las matemáticas. Se han demostrado muchos resultados parciales y casos especiales, y se sigue trabajando para encontrar una demostración completa o para comprender mejor la conjetura.



Hay mucha gente que ya los resolvió, conozco a alguien que incluso ya lo demostró en la universidad local y tiene su apoyo de los matemáticos.Pero hasta ahí llegó,le piden publicar en una revista científica.Pero ninguna revista quiere siquiera mirarlo, la respuesta es la sgte hay muchas personas que dicen que lo resolvieron y ya no revisamos esos trabajo. Es como una respuesta automática que dan las revistas, entonces como será posible que lo den a conocer??? Estoy convencida que no solo el resolvió un problema ,si no que también existen personas en el mundo que tampoco pudieron llegar a publicarlo .En YouTube está su demostración por si quieren ver…Marco Burgos Hipótesis de Rieman también está cargado en un repositorio.
El usuario también pregunta si hay valores donde la serie es cero para un medio, lo que interpreto como preguntar si hay valores de p p y s s tales que ∑k=0∞ (p(-s))k = 1/2 ∑ k = 0 ∞ ( p − s) k = 1 / 2. Usando la fórmula, esto equivale a resolver 1/(1 – p^(-s)) = 1/2 1 / ( 1 − p − s) = 1/2, que se simplifica a p^(-s) = 1/3 p − s = 1/3. Tomando el logaritmo de ambos lados, obtenemos -s log(p) = log(3) − s log ( p ) = log ( 3), lo que implica que s = -log(3)/log(p) s = − log ( 3) / log ( p). Por lo tanto, para cualquier valor de p p tal que 0 < p 1, existe un valor correspondiente de s s que hace que la serie sea igual a la mitad.
pues q yo estado resolviendo entodas los tipos q hay pues me salio 1900.0000 el sesultado pero nose si sera la unica razon es ubicar bien las palabras claves