En esta segunda entrada acerca de las cónicas vamos a hablar de la cónica más similar a la circunferencia y quizás la segunda más conocida: la elipse.
Se denomina cónica o sección cónica a la curva resultante de la intersección entre un cono y un plano. Existen cuatro cónicas: circunferencias, elipses, parábolas e hipérbolas.
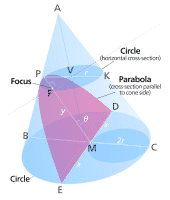
Una elipse se produce cuando un cono se ve cortado por un plano inclinado como puede observarse en la siguiente imagen:
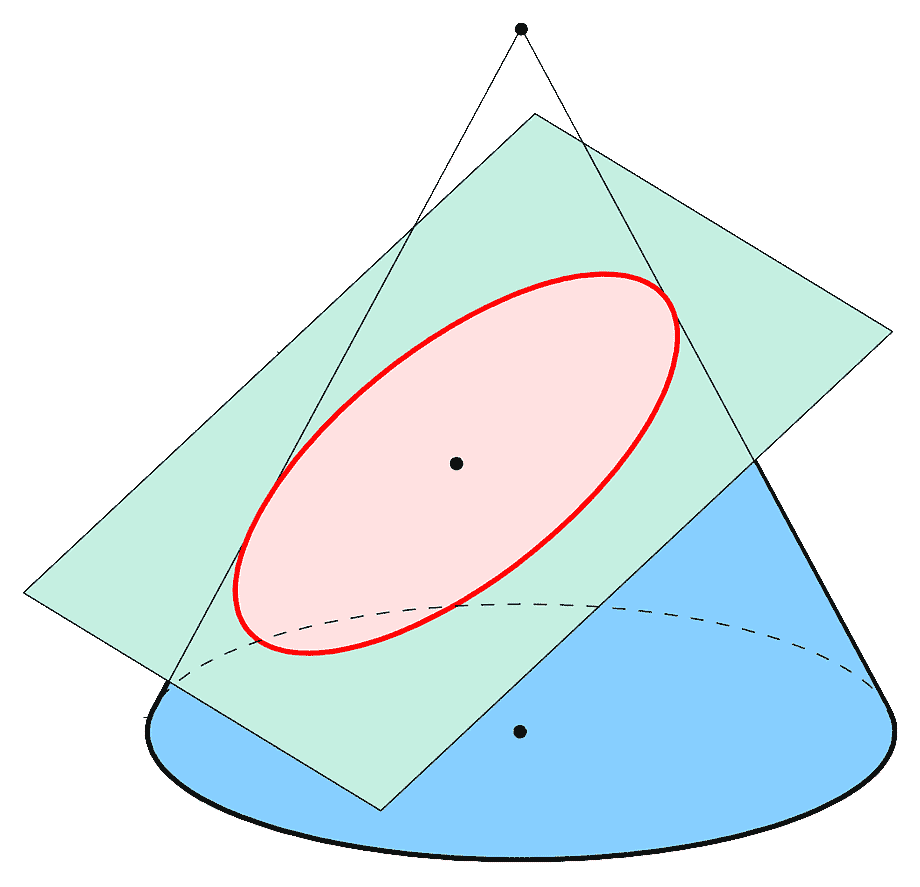
Podría decirse que el caso particular de elipse con ángulo de inclinación del plano nulo produce una circunferencia.
Demostración algebraica de la ecuación de la elipse
Una elipse es el lugar geométrico de los puntos del plano tal que la suma de la distancia entre dicho punto y 2 puntos denominados los focos de la elipse es constante e igual al eje mayor de la elipse.
A continuación se presenta un esquemático de los puntos que cumplen dicha condición (elipse en sí) junto con los focos y la definición de los ejes mayor y menor de la elipse:
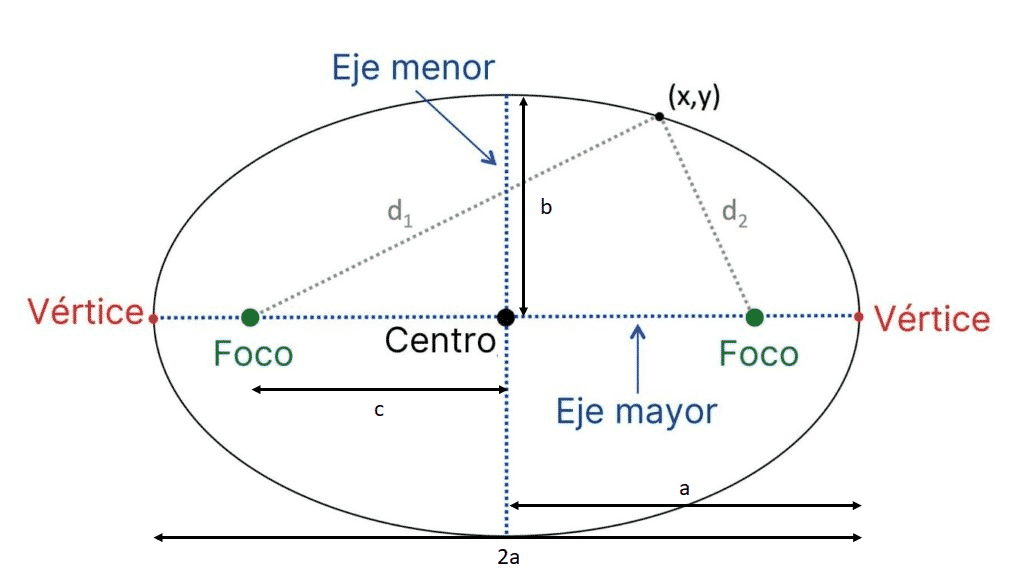
Las dimensiones fundamentales de una elipse son:
- Semieje mayor: longitud a
- Semieje menor: longitud b
- Semidistancia focal: c
De dicho esquema puede deducirse fácilmente 2 consideraciones:
- La suma de las distancias de un punto de la elipse (d1+d2) es igual al eje mayor 2a. Esto se produce cuando el punto se encuentra en un vértice de la elipse ya que la suma de las distancias comprende el eje mayor.
- Cuando el punto se encuentra en la parte superior se tiene un triángulo que puede descomponerse en dos triángulos rectángulos como puede comprobarse en la imagen de abajo. Como la suma de las distancias es 2a y en cada triángulo rectángulo hay la mitad de dicha distancia (a) debido a la simetría, por pura trigonometría se deduce que \(b^{2}+c^{2}=a^{2}\)
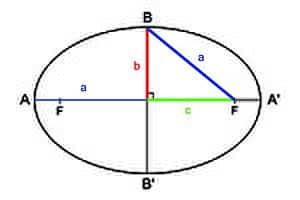
Esta última relación \(b^{2}+c^{2}=a^{2}\) es muy importante para poder obtener la ecuación algebraica de una elipse en base a las dimensiones de sus semiejes a y b y no en base a la semidistancia focal c que no aporta mucha información.
Volviendo a la figura esquemática, nos interesa saber las coordenadas de los 3 puntos que nos van a garantizar obtener la ecuación algebraica en términos de las variables x e y. Los puntos son:
- Punto genérico de la curva elíptica (x,y)
- Punto del foco derecho (c,0)
- Punto del foco izquierdo (-c,0)
Siendo \(d_{1}\) y \(d_{2}\) la distancia del punto en la elipse a los focos como denota el esquemático, la propiedad de la elipse nos dice que:
\(d_{1}+d_{2}=2a\)
Se recuerda que la distancia entre dos puntos en un plano se obtiene de la siguiente manera:
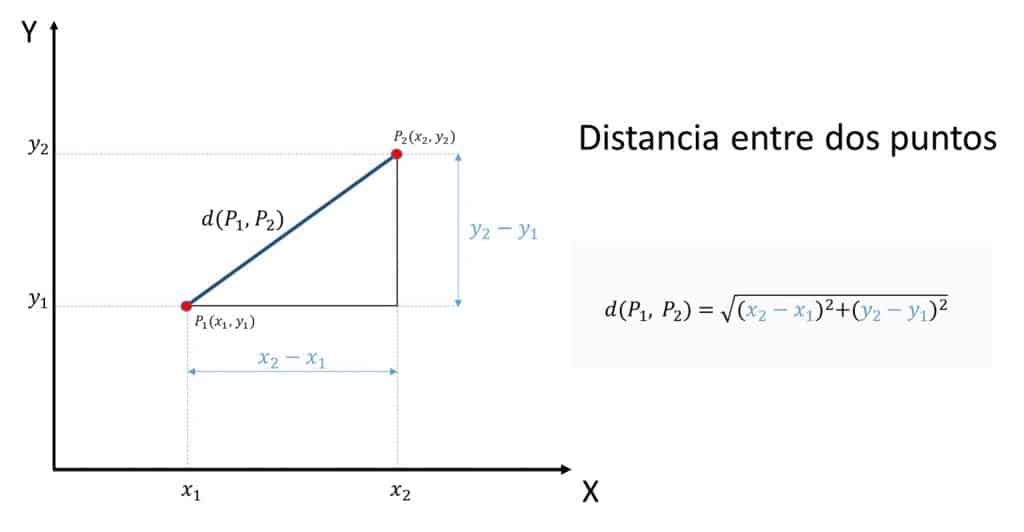
Por lo tanto las distancias son:
- \(d_{1} = \sqrt{(x+c)^{2} + y^{2}}\)
- \(d_{2} = \sqrt{(x-c)^{2} + y^{2}}\)
La ecuación general que debemos simplificar resulta:
\(\sqrt{(x+c)^{2} + y^{2}} + \sqrt{(x-c)^{2} + y^{2}} = 2a\)
Reordenando términos:
\(\sqrt{(x-c)^{2} + y^{2}} = 2a – \sqrt{(x+c)^{2} + y^{2}}\)
Elevando al cuadrado:
\((x-c)^{2} + y^{2} = 4a^{2} + (x+c)^{2} + y^{2} -4a\sqrt{(x+c)^{2} + y^{2}}\)
Desarrollando los paréntesis:
\(x^{2} + c^{2} -2xc + y^{2} = 4a^{2} + x^{2} + c^{2} + 2xc + y^{2} -4a\sqrt{(x+c)^{2} + y^{2}}\)
Eliminando términos:
\(4a\sqrt{(x+c)^{2} + y^{2}} = 4a^{2} + 4xc\)
Dividimos entre 4 y elevamos al cuadrado:
\(a^{2} [(x+c)^{2} + y^{2}]= a^{4} + x^{2}c^{2} + 2a^{2}xc\)
Desarrollando los paréntesis:
\(a^{2}x^{2} + a^{2}c^{2} + 2a^{2}xc + a^{2}y^{2} = a^{4} + x^{2}c^{2} + 2a^{2}xc\)
Eliminando términos y agrupando:
\(x^{2} (a^{2}-c^{2}) + y^{2}a^{2} = a^{2}(a^{2}-c^{2})\)
De la relación \(a^{2} = b^{2} + c^{2}\) sacamos que \(a^{2} – c^{2} = b^{2}\):
\(x^{2}b^{2} + y^{2}a^{2} = a^{2}b^{2}\)
Por último sólo nos queda dividir ambos lados de la ecuación por \(a^{2}b^{2}\) para obtener la ecuación final:
\(\dfrac{x^{2}}{a^{2}} + \dfrac{y^{2}}{b^{2}} = 1\)
Dicha ecuación sólo es válida cuando el origen de la elipse se encuentra en el origen de coordenadas y además los ejes se encuentran alineados con los ejes de coordenadas. De lo contrario (elipse girada o centro fuera del origen de coordenadas) la ecuación se complica algo más.
Para la elipse girada es necesario un desarrollo sencillo pero muy avanzado matemáticamente hablando que se sale del objetivo del artículo, aunque en este enlace se explica, y para el caso descentrado bastaría con hacer el mismo desarrollo pero considerando un punto central genérico (\(x_{0},y_{0}\)) tal que:
- Punto genérico de la curva elíptica (\(x,y\))
- Punto del foco derecho (\(x_{0}+c,y_{0}\))
- Punto del foco izquierdo (\(x_{0}-c,y_{0}\))
Sin embargo no es necesario hacer el desarrollo de nuevo. Si hacemos un cambio de variable (o de notación más bien) considerando el punto genérico como:
- \(x’=x-x_{0}\)
- \(y’=y-y_{0}\)
Se tiene que al restar las coordenadas para calcular la distancia entre los puntos se llega a la misma ecuación en términos de las nuevas variables:
\(\sqrt{(x’+c)^{2} + y’^{2}} + \sqrt{(x’-c)^{2} + y’^{2}} = 2a\)
Por lo tanto el desarrollo sería idéntico y se llegaría a:
\(\dfrac{x’^{2}}{a^{2}} + \dfrac{y’^{2}}{b^{2}} = 1\)
Si devolvemos el cambio de variable de nuevo a las coordenadas genéricas x e y queda:
\(\dfrac{(x-x_{0})^{2}}{a^{2}} + \dfrac{(y-y_{0})^{2}}{b^{2}} = 1\)
2 últimas consideraciones:
- Si ambos focos se encontrasen en el centro, es decir, c=0, entonces se tendría que a=b y se obtendría la ecuación de la circunferencia.
- En ningún momento se ha tenido cuidado con dividir términos y obtener cuadrados de raíces sin poner valor absoluto porque se han asumido las dimensiones a,b y c positivas y mayores a 0.
Parametrización de la elipse
En la ecuación anterior tenemos una restricción y 2 variables. Es decir, una curva. Es problemático querer pintar dicha curva empleando directamente las variables x e y ya que, si queremos ir variando x por ejemplo, debemos de calcular el valor de y que debe de coincidir en todo momento con el valor esperado. Y como podréis comprobar, hay raíces de por medio, de forma que si no operamos con el cuidado necesario acabaremos pintando sólo media elipse (Que es lo que ocurre si intentamos generar una gráfica y=f(x) para representar la elipse).
Para solucionar este problema recurrimos a una parametrización. De esta forma, las variables x e y se relacionan de forma que variando una tercera variable obtenemos el valor esperado de x e y automáticamente. Para ello empleamos las coordenadas polares.
Recordamos la fórmula fundamental de la trigonometría: \(cos ^{2} (\theta)+ sen ^{2} (\theta) = 1\)
Muy similar a la ecuación de la elipse. Para que se cumplan ambas ecuaciones considerando la elipse descentrada debemos hacer que:
- \(\dfrac{(x-x_{0})^{2}}{a^{2}} = cos ^{2} (\theta)\)
- \(\dfrac{(y-y_{0})^{2}}{b^{2}} = sen ^{2} (\theta) \)
Es decir que el cambio de variables necesario resulta:
\(\left\{\begin{matrix} x=x_{0} + a*cos(\theta) \\ y=y_{0} + b*sen(\theta) \end{matrix}\right\) , con \(0 \leq \theta \leq 2\pi\)
De esta forma pintamos la elipse en sentido antihorario comenzando por el eje x. Podríamos intercambiar el seno y el coseno y/o añadir desfase para cambiar la forma en la que «pintamos» la elipse.
Propiedad focal de la elipse
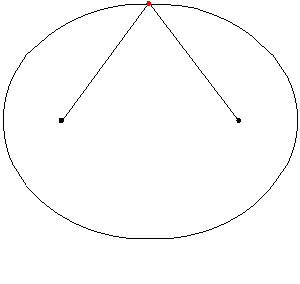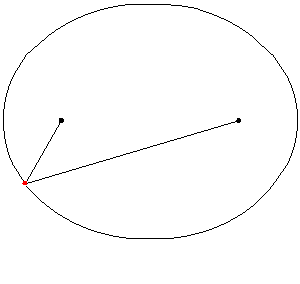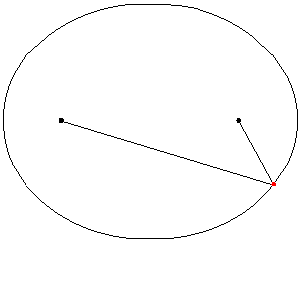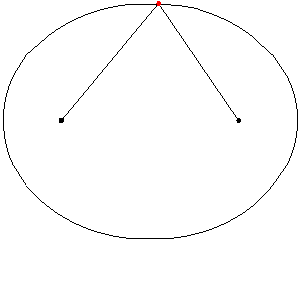
En cada punto de la elipse, la recta tangente a la curva forma ángulos iguales con los segmentos que unen el punto con los focos como muestra la siguiente imagen:
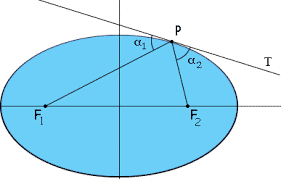
Ello implica, por ejemplo, que si la curva de la elipse fuese un espejo, al emitir un rayo hacia cualquier dirección desde uno de los focos el rayo siempre rebotará y llegará por reflexión al otro foco como muestra la siguiente imagen:
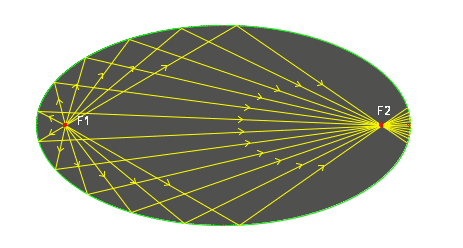
Esto tiene una utilidad ENORME y se tienen por ejemplo dos aplicaciones prácticas:
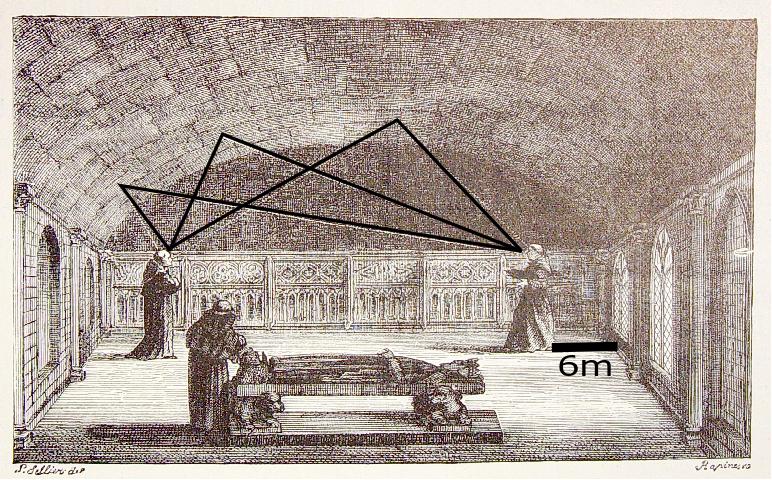
- En las denominadas galerías de los murmullos. Si sois curiosos y habéis viajado y visitado museos de ciencias probablemente habéis visto como, en cierta habitación con agujeros, puedes hablar bajo en un agujero de la pared y te escucha perfectamente otra persona que se encuentre en el extremo opuesto, como si existiera una especie de altavoz. En edificios antiguos se denomina galería de los murmullos y servía para que personas alejadas pudiesen hablar sin gritarse, y en museos probablemente habréis visto una especie de antena con forma de elipsoide cortado (un elipsoide es una revolución de una elipse y conserva sus propiedades focales tridimensionalmente) tal que si hablas en el foco te escucha otra persona claramente a una distancia considerable.
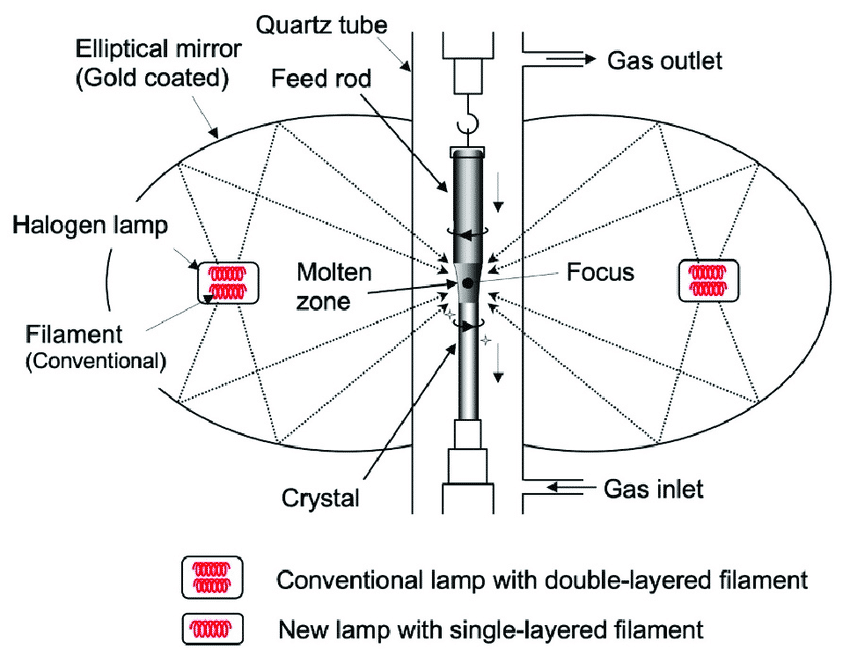
- Otra aplicación bastante importante es un horno elíptico. Si se coloca la fuente de calor en un foco y lo que queremos calentar en el otro foco, absolutamente toda la radiación infrarroja («calor») emitida por el horno irá hacia el objeto a calentar de forma que podemos focalizar o concentrar el calor sobre un punto y además de manera uniforme porque los rayos llegarán por todas las direcciones y no sólo por una franja o línea de visión.


Gracias. Muy Bueno.
Gracias