¿Qué es la curva tautócrona?
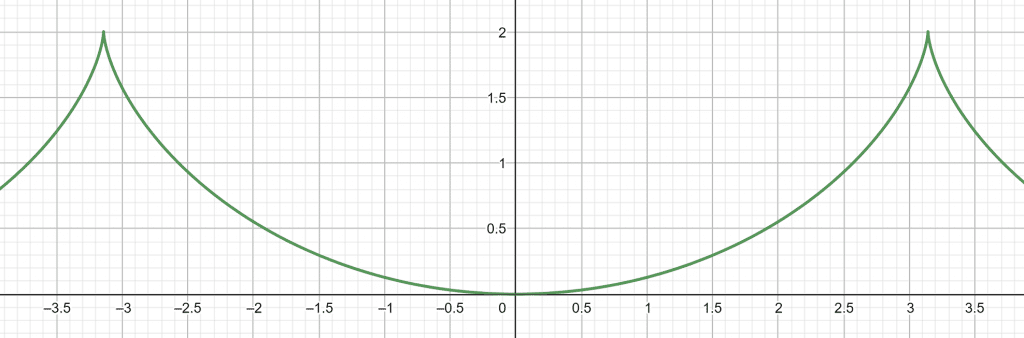
La curva tautócrona o curva isócrona es la curva para la cual, el tiempo que tarda un objeto deslizando por ella sin rozamiento con gravedad constante hasta el punto más bajo, es independiente de la posición inicial. El nombre se compone de los prefijos griegos tauto- que significa mismo o iso- igual, y chrono tiempo.
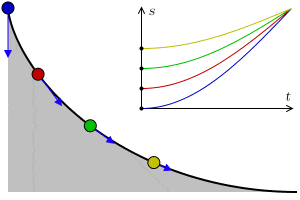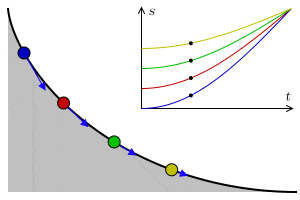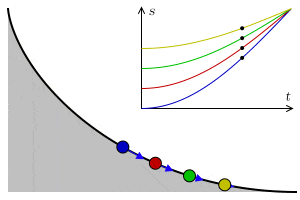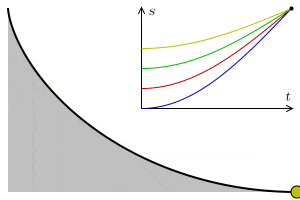
Esta curva, sorprendentemente, es también una cicloide, como ocurre con la curva braquistócrona. Es decir, que la cicloide es la curva que permite descender más rápido entre dos puntos no alineados y además tiene la propiedad de que el origen no influye en el tiempo de llegada.
Historia de la curva tautócrona
El primer registro de una demostración exitosa de que la curva tautócrona es una cicloide data del año 1659 por parte de Christiaan Huygens en su obra Horologium Oscillatorium. Esta se considera una de las tres obras más importantes sobre mecánica del siglo XVII, siendo las otras dos la de Galileo de Discursos y demostraciones matemáticas relativas a dos nuevas ciencias (1638) y la de Isaac Newton Philosophiæ Naturalis Principia Mathematica (1687).
En una cicloide cuyo eje se eleva sobre la perpendicular y cuyo vértice está localizado en el fondo, el tiempo de descenso en el cual un cuerpo llega al punto más bajo, al vértice, después de haber partido desde cualquier punto de la cicloide, es igual a cualquier otro.
Christiaan Huygens
Huygens estudió más de cerca el problema de la tautócrona cuando se dio cuenta de que un péndulo, que sigue una trayectoria circular, no era isócrono y, por lo tanto, su reloj de péndulo mantendría un tiempo diferente dependiendo de cuánto se balancease el péndulo.
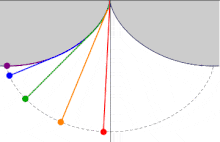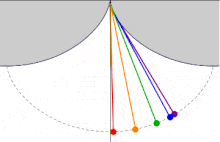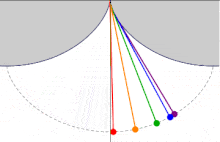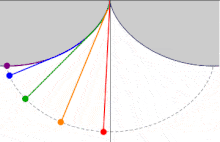
Después de determinar la curva correcta, Christiaan Huygens intentó crear relojes de péndulo modificados para que el péndulo recorriese una curva tautócrona o cicloide. Estos intentos resultaron inútiles porque la fricción de la cuerda causaba una disminución de la frecuencia y además otros factores añadían errores a la medición. No obstante, descubrió que el «error circular» de un péndulo disminuye al disminuir la longitud del arco de giro, por lo que escapes de reloj podían emplearse para reducir al máximo la inexactitud.
Demostración matemática de la curva tautócrona: Solución de Abel
Numerosas demostraciones algebraicas y geométricas han puesto de manifiesto que la cicloide es una curva que cumple la propiedad de la tautócrona. No obstante, lo complicado y bello es demostrar que la única curva que cumple la propiedad de la tautócrona es la cicloide. Esta demostración fue realizada por primera vez por Niels Henrik Abel, quien estudió su propio problema, el problema mecánico de Abel, con la peculiaridad de que el tiempo de llegada es una constante independiente de la altura.
Supongamos que tenemos una curva genérica (podría incluso tener cambios de pendiente/oscilaciones) sobre la cual se encuentra en reposo una partícula a una altura \(y_{0}\). Entonces se deja rodar por acción de la gravedad sin rozamiento hasta que llega al final de la curva, es decir, el origen de coordenadas.
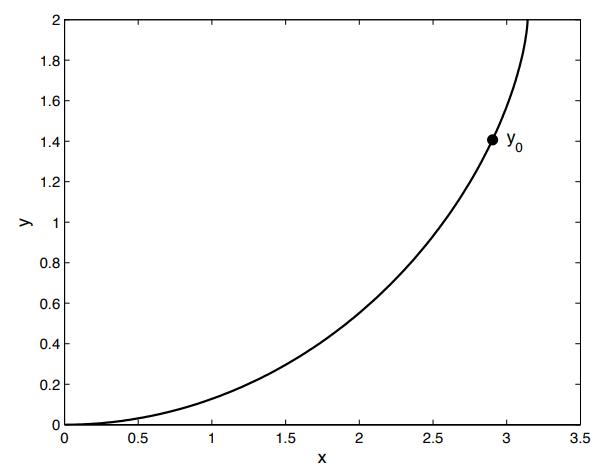
Por conservación de la energía mecánica, se debe de tener la siguiente equivalencia:
\(mgy_{0} = \dfrac{1}{2} V^{2}(y) + mgy\)
Agrupando términos y definiendo la velocidad en función de la distancia de la curva recorrida \(s\):
\(\dfrac{1}{2} \left (\dfrac{ds}{dt} \right )^{2} = mg(y_{0}-y)\)
Despejando:
\(\dfrac{ds}{dt} = \pm \sqrt{2 g (y_{0} – y)} \)
\(dt = \pm \dfrac{ds}{\sqrt{2 g (y_{0} – y)}} \)
\(dt = – \dfrac{1}{\sqrt{2 g (y_{0} – y)}} \dfrac{ds}{dy} dy \)
El término \(\dfrac{ds}{dy}\) indica cómo varia la distancia total recorrida \(s(y)\) a medida que aumenta la altura \(y\). Como obviamente la partícula está cayendo, la derivada va a ser siempre negativa, es decir, a menor altura mayor es la distancia recorrida. Por otra parte, el radicando de la raíz siempre es positivo porque la altura siempre va a disminuir, por lo que no hay ningún problema de posibilidad de obtener números complejos y con todo esto podemos asegurar el signo negativo para obtener un tiempo real positivo a la izquierda de la ecuación.
El tiempo total de caída vendrá dado por la siguiente integral:
\(\displaystyle T(y_{0}) = \int_{y_{0}}^{0} dt = \dfrac{1}{\sqrt{2g}} \int_{0}^{y_{0}} \dfrac{1}{\sqrt{y_{0} – y}} \dfrac{ds}{dt} dy\)
Esta es la ecuación integral de Abel que permite calcular el tiempo empleado en caer dada la forma de la curva \(s(y)\) y por lo tanto su derivada \(\dfrac{ds}{dt}\). No obstante, el objetivo del problema mecánico de Abel es el opuesto: dado un tiempo de caída \(T(y_{0})\), queremos encontrar el \(\dfrac{ds}{dt}\) que verifique la ecuación.
Convolución
Para poder resolver la integral antes es necesario recordar lo que es la convolución. Una convolución es un operador matemático que transforma dos funciones f y g en una tercera función que en cierto sentido representa la magnitud en la que se superponen f y una versión trasladada e invertida de g.
Se define como la integral del producto de ambas funciones después de desplazar una de ellas a lo largo del dominio. Es decir, si el dominio es el temporal, la convolución de las funciones mencionadas tendría la forma:
\(\displaystyle (f*g)(t)\ {\stackrel {{\mathrm {.}}}{=}}\int _{{-\infty }}^{{\infty }}f(\eta )g(t-\eta )d\eta\)
Tranformada de Laplace
Por otra parte, la Transformada de Laplace es una transformada integral que convierte una función de variable real (normalmente el tiempo) a una función de variable compleja. Tiene muchas aplicaciones en ciencia e ingeniería porque es una herramienta para resolver ecuaciones diferenciales. En particular, transforma ecuaciones diferenciales en ecuaciones algebraicas.
La transformada de cada función sigue un cierto patrón al igual que ocurre con las derivadas de las funciones, siendo las principales transformadas las que se muestran en la siguiente tabla:
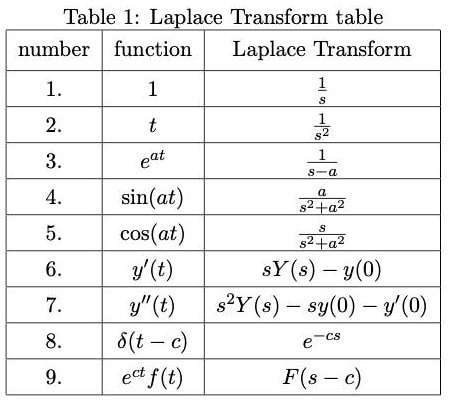
La utilidad de la Transformada de Laplace se debe a que, tras pasar la función al dominio complejo de Laplace, las funciones adquieren unas propiedades muy interesantes que permiten simplificar problemas y, tras simplificar el problema, basta con volver al dominio real para obtener la solución buscada.
Una de las propiedades que cumple la Transformada de Laplace es que, la Transformada de Laplace de una convolución es igual al producto de las transformadas de Laplace de cada función, es decir:
\({\displaystyle {\mathcal {L}}\{f(t)*g(t)\}={\mathcal {L}}\{f(t)\}{\mathcal {L}}\{g(t)\}}\)
Resolución de la integral del Problema mecánico de Abel
Recordemos que la integral que buscamos resolver es:
\(\displaystyle \dfrac{1}{\sqrt{2g}} \int_{0}^{y_{0}} \dfrac{1}{\sqrt{y_{0} – y}} \dfrac{ds}{dy} dy\)
Podemos identificar dos funciones:
\( f(y) = \dfrac{ds}{dy}\) \( g(y) = \dfrac{1}{\sqrt{y}}\)Cuya convolución da:
\(\displaystyle \dfrac{1}{\sqrt{2g}} \cdot (f * g)(y) = \dfrac{1}{\sqrt{2g}} \cdot \int_{0}^{y_{0}} \dfrac{1}{\sqrt{y_{0} – y}} \dfrac{ds}{dy} dy\)
Por lo tanto:
\(\displaystyle \mathcal {L} [T(y_{0})]= \dfrac{1}{\sqrt{2g}} \mathcal {L} \left [\dfrac{ds}{dy} \right ] \mathcal {L} \left [\dfrac{1}{\sqrt{y}} \right ] \)
Como el tiempo es una función constante independiente del punto inicial, \(T(y_{0}) = T_{0}\), las transformadas de las funciones en juego son:
\(\mathcal {L} [T(y_{0})] = T_{0} \dfrac{1}{z} \) \(\mathcal {L} \left [\dfrac{1}{\sqrt{y_{0}}} \right ] = \sqrt{\pi} z^{-1/2} \)Despejando la Transformada de Laplace incógnita \(\mathcal {L} \left [\dfrac{ds}{dy} \right ]\):
\(\mathcal {L} \left [\dfrac{ds}{dy} \right ] = \sqrt{2g} \dfrac{\mathcal {L} [T(y_{0})]}{\mathcal {L} \left [\dfrac{1}{\sqrt{y}} \right ]} = \sqrt{\dfrac{2g}{\pi}} T_{0} z^{-1/2}\)
Una vez tenemos la Transformada de Laplace de la función que queremos obtener, basta con aplicar la anti-transformada, de forma que obtenemos:
\(\dfrac{ds}{dy} = T_{0} \dfrac{\sqrt{2g}}{\pi} \dfrac{1}{\sqrt{y}}\)
Un diferencial de curva \(ds\) se relaciona con las coordenadas (x,y) como:
\(ds = \sqrt{(dy)^{2} + (dx)^{2}}\)
De esta forma, la derivada con respecto a \(y\) puede escribirse como:
\(\dfrac{ds}{dy} = \sqrt{1 + \left (\dfrac{dx}{dy} \right )^{2}}\)
Agrupando los términos con una constante \(K = \dfrac{2gT_{0}^{2}}{\pi}\) y sustituyendo el valor de \(\dfrac{ds}{dy}\) obtenido:
\(\displaystyle \sqrt{\dfrac{K}{y}} = \sqrt{1 + \left (\dfrac{dx}{dy} \right )^{2}}\)
\(\displaystyle \dfrac{dx}{dy} = \sqrt{\dfrac{K-y}{y}}\)
\(\displaystyle x(y) = \int \sqrt{\dfrac{K-y}{y}} dy\)
Haciendo el cambio de variable:
\(\begin{cases} y = K sin^{2}(t) \ \rightarrow \ K – y = K(1-sin^{2}(t)) = Kcos^{2}(t) \\ dy = 2K sin(t) cos(t) dt \end{cases}\)\(\displaystyle x(y) = \int \sqrt{\dfrac{cos^{2}(t)}{sin^{2}(t)}} 2K sin(t) cos(t) dt = 2K \int cos^{2}(t) dt\)
\(\begin{cases} x(t) = K \left (t + \dfrac{sin(2t)}{2} \right ) \\ y(t) = K sin^{2}(t) \end{cases} \)
Si operamos un poco con las funciones trigonométricas obtenemos la siguiente solución equivalente:
\(\begin{cases} x(t) = \dfrac{K}{2} \left (2t +sin(2t) \right ) \\ \\y(t) = \dfrac{K}{2}(1-cos(2t)) \end{cases} \)La cual, al igual que pasaba con la braquistócrona, es la ecuación de una cicloide. La diferencia en la solución (seno positivo) es debida a que en este caso la ecuación es de una cicloide hacia abajo mientras que con la braquistócrona aparecía una cicloide normal. Esto se debe a la forma en la que hemos establecido la parametrización de la curva.