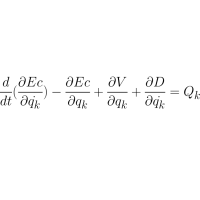Seguro que todos conocemos la fórmula de la energía mecánica de un cuerpo: Energía cinética + Energía potencial. En este artículo vamos a responder a un par de preguntas:
- ¿Por qué la energía mecánica es la suma de dichas energías?
- ¿De dónde aparece la energía cinética?
- ¿Qué es eso del potencial y cómo se obtiene la expresión de dicha energía?
Energía cinética. Teorema de las fuerzas vivas
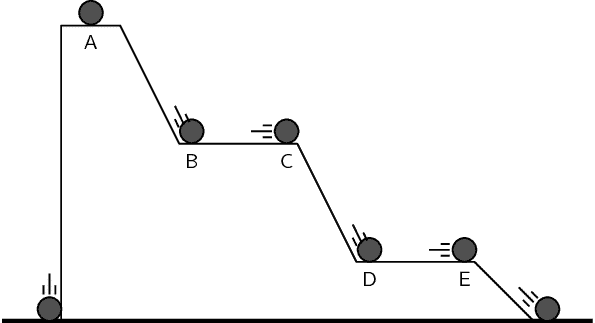
La energía cinética de un cuerpo representa la energía que posee debido al movimiento. Se define como el trabajo necesario para acelerar un cuerpo de una masa determinada desde el reposo hasta una velocidad determinada.
Cuando una fuerza actúa, genera una aceleración que es proporcional a la fuerza e inversamente proporcional a la masa del cuerpo. \(\overrightarrow{a}=\frac{\overrightarrow{F}}{m}\). Dicha aceleración genera una velocidad que induce al movimiento, siendo esta la energía cinética generada por la fuerza, tal que para poder disminuirla hay que ejercer fuerza en el sentido contrario.
El teorema de las fuerzas vivas dice:
El trabajo total \(W\) realizado por la suma de todas las fuerzas aplicadas a una partícula es igual al cambio que experimenta la energía cinética de dicha partícula \( \bigtriangleup Ec\)
Que podemos completar diciendo:
La potencia realizada por la suma de todas las fuerzas aplicadas a una partícula \(\frac{dW}{dt}\) es igual a la variación respecto al tiempo de la energía cinética \(\frac{dEc}{dt}\)
Es decir:
\(W_{Total}= \bigtriangleup Ec=Ec_{2}-Ec_{1}=\frac{1}{2}*m*(v_{2}^{2}-v_{1}^{2})\)Pero, ¿De dónde se obtiene dicha fórmula?. Vamos a deducirla partiendo, casi como en el 80% de los casos, de la 2º Ley de Newton. Además emplearemos la fórmula del trabajo.
Demostración
\(\sum \overrightarrow{F}=m*\overrightarrow{a}\) \(\int_{1}^{2}dW=\int_{r1}^{r2} \overrightarrow{F} *d \overrightarrow{r}\) \(P= \frac{dW}{dt} = \overrightarrow{F}* \overrightarrow{v} \)Combinando las expresiones tal que \( \overrightarrow{a} = \frac{d\overrightarrow{v}}{dt} \) y \( \overrightarrow{v} = \frac{d\overrightarrow{r}}{dt} \)
\(\frac{dW}{dt}=\overrightarrow{F}*\overrightarrow{v}=m*\overrightarrow{a}* \overrightarrow{v}=m*\frac{d \overrightarrow{v}}{dt}* \overrightarrow{v} =\frac{1}{2}*m*\frac{d \overrightarrow{v}^{2} }{dt}=\frac{d(\frac{1}{2}*m*v^{2})}{dt}=\frac{dEc}{dt}\)Hay otra forma que no emplea la potencia y genera directamente la relación entre trabajo y energía cinética; no obstante matemáticamente no queda tan elegante como la primera, la cual emplearemos en sucesivas demostraciones.
\(\int_{1}^{2}dW=\int_{r1}^{r2} m*\overrightarrow{a} *d \overrightarrow{r}= \int_{r1}^{r2} m\frac{d\overrightarrow{v}}{dt} *d \overrightarrow{r}= \int_{v1}^{v2} d \overrightarrow{v}* \frac{d\overrightarrow{r}}{dt} = \) \(= \int_{v1}^{v2} m* \overrightarrow{v} *d \overrightarrow{v} = \frac{1}{2}*m*(v_{2}^{2}-v_{1}^{2}) = \bigtriangleup Ec \)Teniendo en cuenta la siguiente equivalencia:
\( {\displaystyle {\frac {d(v^{2})}{dt}}\,={\frac {d({\vec {v}}\,.\,{\vec {v}})}{dt}}={\frac {d{\vec {v}}}{dt}}\,.\,{\vec {v}}+{\vec {v}}\,.\,{\frac {d{\vec {v}}}{dt}}=2\,{\frac {d{\vec {v}}}{dt}}\,.\,{\vec {v}}=2\,{\vec {a}}\,.\,{\vec {v}}}\)Casos en los que no varía la energía cinética
Esto ocurre cuando \(\overrightarrow{F}* \overrightarrow{v}=0 \) con:
- \(\overrightarrow{F}=0\) —–> Primera Ley de Newton
- \(\overrightarrow{v}=0\) —–> Si no hay variación de posición no hay trabajo.
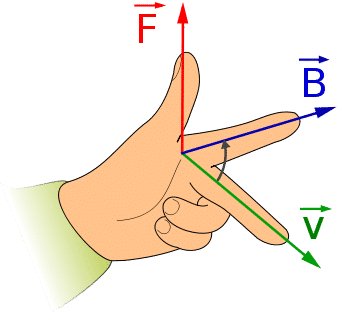
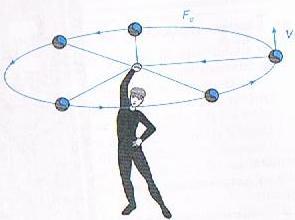
- \(\overrightarrow{F} \perp \overrightarrow{v}\) ——> Ocurre en el caso de la fuerza magnética o durante un MCU
Energía potencial

La energía potencial es un tipo de energía mecánica «almacenada», asociada a la localización de un cuerpo dentro de un campo de fuerzas conservativas.
Una fuerza es conservativa cuando el trabajo que realiza es igual a la diferencia entre los valores inicial y final de una función que sólo depende de las coordenadas finales e inicial. Dicha función se denomina potencial.
\(\overrightarrow{F}(r)=-\overrightarrow{\bigtriangledown}V(r)=-\frac{dEp}{dr}\)Ejemplo: Energía potencial gravitatoria
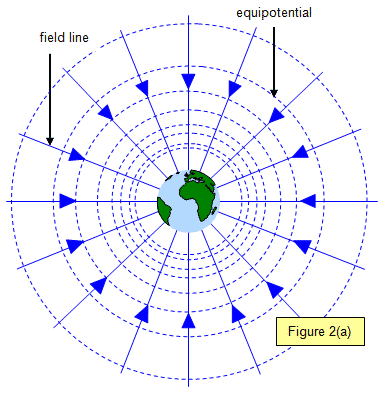
La fuerza gravitatoria es: \(\overrightarrow{F}=-\frac{G*M*m}{r^{3}}*\overrightarrow{r}\)
\(-\int_{A}^{B}dEpg=\int_{r_{a}}^{r_{b}} -\frac{G*M*m}{r^{2}}*dr\)Para poder obtener una expresión directa (sin expresar un incremento) de la energía potencial debemos de elegir un punto de referencia como origen de potencial 0. Se escoge el infinito, donde la acción de las fuerzas es nula, y se define la energía potencial como la energía necesaria para llevar una masa desde el infinito hasta un punto A.
\(-\int_{\infty}^{A}dEpg=\int_{\infty}^{r_{a}} -\frac{G*M*m}{r^{2}}*dr\)\(Epg_{A}-Epg_{\infty}=-\frac{G*M*m}{r_{a}}+ \frac{G*M*m}{\infty} \). Que para el caso general:
\(Epg= -\frac{G*M*m}{r} \)El signo negativo tiene sentido, ya que para mover una carga desde el infinito no hace falta aportar energía, sino que se desarrollaría un trabajo. Expresándolo de esta manera, el trabajo necesario para mover una carga de un punto A a otro B es igual al incremento de energía potencial: \(W=Epg_{B}-Epg_{A}\)
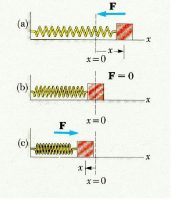
Ejemplo: Energía potencial elástica
La fuerza elástica es \(\overrightarrow{F}=-k*x\)
\(-\int_{A}^{B}dEpe=\int_{x_{a}}^{x_{b}}-k*x*dx\)Escogiendo como punto de potencial 0 el punto de equilibrio, tal que x representa el incremento de longitud respecto a dicho punto, el potencial en x=0 es 0.
\(-\int_{0}^{A}dEpe=\int_{0}^{x_{a}} -k*x*dx\)\(Epe_{A}-Epe_{0}=\frac{1}{2}*k*x_{a}^{2}- \frac{1}{2}*k*0^{2} \). Que para el caso general:
\(Epe=\frac{1}{2}*k*x^{2}\)Energía mecánica

La energía mecánica es la energía asociada al movimiento y/o posición de los cuerpos. Esto incluye a la suma de la energía cinética y a la energía potencial asociada a las fuerzas conservativas (Gravitatoria, elástica, electrostática).
Se conocen dos teoremas:
- Si sobre un cuerpo sólo actúan fuerzas conservativas, la energía mecánica del sistema permanece constante. \(\bigtriangleup Em=0\)
- La variación de la energía mecánica de un cuerpo es igual al trabajo realizado por las fuerzas no conservativas. \(\bigtriangleup Em= \bigtriangleup W_{nc}\)
Vamos a demostrar ambos teoremas.
Todas la fuerzas son conservativas
\(\frac{dW}{dt}=\frac{dEc}{dt}=\overrightarrow{F}*\overrightarrow{v}=-\frac{dEp}{dr}*\frac{dr}{dt}= -\frac{dEp}{dt}=\frac{dEc}{dt}\) \(\frac{dEc}{dt}+\frac{dEp}{dt}=\frac{d(Ep+Ec)}{dt}=0 \rightarrow Ec+Ep=cte=E_{mec} \rightarrow\bigtriangleup E_{mec}=0\)Existen fuerzas conservativas y no conservativas
\(\frac{dW}{dt}=\frac{dEc}{dt}=(\overrightarrow{F}_{c}+ \overrightarrow{F}_{nc})*\overrightarrow{v}=-\frac{dEp}{dr}*\frac{dr}{dt}+\frac{dW_{nc}}{dt}= -\frac{dEp}{dt} +\frac{dW_{nc}}{dt} =\frac{dEc}{dt}\) \(\frac{dEc}{dt}+\frac{dEp}{dt}= \frac{dW_{nc}}{dt}=\frac{d(Ep+Ec)}{dt}; \rightarrow \rightarrow \bigtriangleup E_{mec}= \bigtriangleup W_{nc}\)Esto ha sido todo. Si tenéis alguna duda o queréis agradecer el contenido os espero en los comentarios. ¡Un saludo!

![Demostración de la ecuación de Bernoulli [Fluidos] Portada Bernoulli](https://ingenieriabasica.es/wp-content/uploads/2020/08/Portada-Bernoulli-200x200.jpg)