En este artículo se presenta la solución detallada paso por paso del examen de Matemáticas II que cayó en Junio de 2024 en Andalucía en Selectividad (PEvAU).
Enunciado


Ejercicio 1

Apartado a)
Para que dos rectas sean paralelas, estas deben de tener la misma pendiente. La pendiente de la recta que une los puntos \(A\) y \(B\) vendría dada por:
\(m = \dfrac{\bigtriangleup y}{\bigtriangleup x} = \dfrac{1-0}{e-1} = \dfrac{1}{e-1}\)
Cuando calculamos la derivada de una función, estamos calculando el valor de la pendiente de la recta tangente en dicho punto de la función. Si calculamos la derivada de la función:
\(f'(x) = \dfrac{1}{x}\)
Por lo tanto, el punto o puntos de \(f(x)\) en los cuales se cumple la condición de paralelismo se da cuando:
\(f'(x) = \dfrac{1}{x} = \dfrac{1}{e-1} \ , \ \ x \in (0, \infty)\)
Esto ocurre con \(\boxed{x = e-1}\), y sólo en dicho punto. Las coordenadas de dicho punto, que vamos a llamar \(C\) son
\(\displaystyle C(e-1,\ln(e-1))\)
Apartado b)
La recta tangente a una función en un punto \(a\) se define como:
\( y = f(a) + f'(a)(x-a)\)
La recta normal, es aquella perpendicular a la tangente. La fórmula resulta:
\( y = f(a) – \dfrac{1}{f'(a)}(x-a)\)
Por lo tanto, la ecuación de la recta normal para el valor \(x = 1\) (Punto A(1,0)) es:
\( y =-1(x-1) = -x + 1 \rightarrow \boxed{y = -x + 1}\)
Ya que \(f(1) = 0\) y \(f'(1) = 1\)
Ejercicio 2
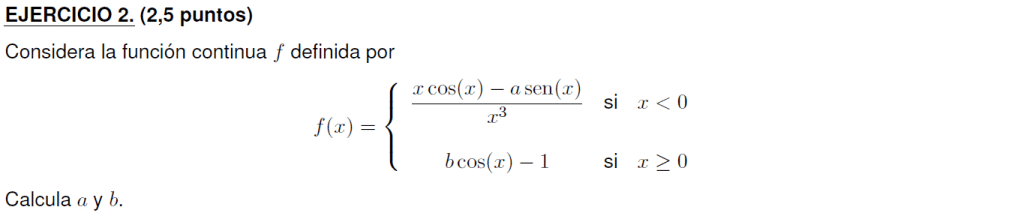
En este ejercicio nos dan una función continua definida a trozos. Nos piden que calculemos a y b. No nos especifican en base a qué, por lo que implícitamente debemos elegir sus valores para que la función sea continua.
Ni la parte superior ni inferior tienen problemas de discontinuidad para valores reales de a y b (no aparecen en ningún denominador, no aparecen en ningún logaritmo o raíz…), por lo que el problema lo vamos a tener en el \( x = 0\). Para que la función sea continua en dicho punto, se debe cumplir que
\(\displaystyle \lim_{x \to 0^{-}} f(x) = \lim_{x \to 0^{+}} f(x)\)
\(\displaystyle \lim_{x \to 0^{-}} f(x) = \lim_{x \to 0} \dfrac{x \cos(x) – a \sin(x)}{x^{3}} = \dfrac{0}{0}\)
Como es una indeterminación, aplicamos la regla de l’Hôpital:
\(\displaystyle \lim_{x \to 0^{-}} f(x) = \lim_{x \to 0} \dfrac{\cos(x) – x \sin(x) – a \cos(x)}{3x^{2}} = \dfrac{1-a}{0}\)
Como queremos que la función sea continua en dicho punto, necesariamente debemos tener que \(\boxed{a = 1}\) para forzar la indeterminación y seguir aplicando L’Hôpital:
\(\displaystyle \lim_{x \to 0^{-}} f(x) = \lim_{x \to 0} \dfrac{-\sin(x) – x \cos(x) }{6x} = \dfrac{0}{0}\)
Aplicamos L’Hôpital de nuevo:
\(\displaystyle \lim_{x \to 0^{-}} f(x) = \lim_{x \to 0} \dfrac{-\cos(x) – \cos(x) + x \sin(x)}{6} = \dfrac{-2}{6} = \dfrac{-1}{3}\)
Vamos a analizar el límite por la derecha:
\(\displaystyle \lim_{x \to 0^{+}} f(x) = \lim_{x \to 0} b \cos(x) – 1 = b – 1\)
Por lo tanto, para que la función sea continua debe cumplirse que:
\(\displaystyle \lim_{x \to 0^{-}} f(x) = \lim_{x \to 0^{+}} f(x) \iff b -1 = \dfrac{-1}{3} \iff \boxed{b = \dfrac{2}{3}} \)
Ejercicio 3

Debemos calcular por lo tanto \(\displaystyle F(x) = \int f(x) dx + C = \int \dfrac{x^{3}+2}{x^{2} – 1} dx\)
Como el integrando es una fracción con polinomios, realizamos una división polinomial para tratar de simplificar el problema.
\(x^{3} + 2 = (x^{2} – 1) x + 2 + x\)
Por lo tanto, nos queda:
\(\displaystyle F(x) = \int x + \dfrac{2 + x}{x^{2} – 1} dx \)
Como el denominador de la segunda integral es de menor orden que el numerador, vamos a dividir la fracción en fracciones simples.
\(\dfrac{2 + x}{x^{2} – 1} = \dfrac{A}{x+1} + \dfrac{B}{x-1} = \dfrac{A(x-1) + B(x+1)}{x^{2} – 1}\)
\(\begin{cases}2 & = B – A \\ 1 & = B + A \end{cases} \rightarrow \begin{cases}A & =-1/2 \\ B & = 3/2 \end{cases}\)Volviendo de nuevo a reformular la integral y dividirla:
\(\displaystyle F(x) = \int x \ dx \ – \dfrac{1}{2} \int \dfrac{1}{x+1} dx + \dfrac{3}{2} \int \dfrac{1}{x-1} dx \)
\(\displaystyle F(x) = \dfrac{x^{2}}{2} – \dfrac{1}{2} \ln|x+1| + \dfrac{3}{2} \ln|x-1| + C \)
La condición que nos dan para determinar la constante es que:
\(F(0) = \boxed{1 = C} \)
Por lo tanto, la función primitiva resulta:
\(\displaystyle \boxed{F(x) = \dfrac{x^{2}}{2} – \dfrac{1}{2} \ln|x+1| + \dfrac{3}{2} \ln|x-1| + 1} \)
Ejercicio 4

En este ejercicio vamos a tener que integrar la función que se nos muestra 2 veces, y para obtener las constantes de integración deberemos de aplicar las condiciones de los puntos.
\( \displaystyle f'(x) = \int x\cos(x) dx + C\)
Para esta primera integral empleamos la regla de integración por partes tal que:
\(\displaystyle \int u \ dv = u \cdot v \ – \int v \ du\)
\(\begin{cases}u & = x \\ dv & = \cos(x) dx \end{cases} \rightarrow \begin{cases}du & = dx \\ v & = \sin(x) \end{cases}\)\( \displaystyle f'(x) = x \sin(x) \ – \int \sin(x) dx = x\sin(x) + \cos(x) + C\)
Volvemos a integrar
\( \displaystyle f(x) =\int \left [ x\sin(x) + \cos(x) + C \right ] dx\)
Para la primera parte de la integral volvemos a aplicar integración por partes:
\(\begin{cases}u & = x \\ dv & = \sin(x) dx \end{cases} \rightarrow \begin{cases}du & = dx \\ v & = -\cos(x) \end{cases}\)\( \displaystyle f(x) =-x \cos(x) + \int \left [\cos(x) + cos(x) + C \right] dx\)
\( \displaystyle f(x) =-x \cos(x) + 2\sin(x) + Cx + D\)
Ahora debemos de sustituir para obtener los valores de las constantes \(C\) y \(K\):
\(\begin{cases}f(0) & = \dfrac{\pi}{2} \\ f(\pi) & = 2 \pi \end{cases} \rightarrow \begin{cases} D& = \dfrac{\pi}{2} \\ C & = \dfrac{1}{2} \end{cases}\)La función buscada resulta:
\(\boxed{f(x) = -x \cos(x) + 2\sin(x) + \dfrac{x}{2} + \dfrac{\pi}{2}}\)
Ejercicio 5

Apartado a)
Este es el típico ejercicio de recurrencia. Consiste en hacer unas cuantas multiplicaciones básicas hasta que identificamos el patrón para extrapolarlo al problema que se nos plantea. Si calculamos \(A^{2}\), \(A^{4}\) y \(A^{8}\):
\(A^{2} = \begin{pmatrix} 1 & 1/8 & 1/8\\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix} 1 & 1/8 & 1/8\\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix} = \begin{pmatrix} 1 & 2/8 & 2/8\\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix}\)
\(A^{4} = \begin{pmatrix} 1 & 2/8 & 2/8\\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix} 1 & 2/8 & 2/8\\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix} = \begin{pmatrix} 1 & 4/8 & 4/8\\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix}\)
\(A^{8} = \begin{pmatrix} 1 & 4/8 & 4/8\\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix} 1 & 4/8 & 4/8\\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix} = \begin{pmatrix} 1 & 8/8 & 8/8\\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix}\)
Llegamos a la conclusión de que:
\(A^{n} = \begin{pmatrix} 1 & n/8 & n/8\\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix}\)
Por lo tanto:
\(\boxed{A^{2024} = \begin{pmatrix} 1 & 253 & 253 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix}}\)
Apartado b)
Nos piden hallar la matrix \(X\) tal que \(A^{2} X A + I = O\). Para despejar la matriz realizamos las siguientes operaciones:
\(A^{2} X A + I = O\)
\(A^{2} X A = -I\)
\( X A = -A^{-2}\)
\( X = -A^{-2} A^{-1} = – A^{-3}\)
Como ya tenemos la fórmula para obtener \( A^{n}\), basta con particularizar para este caso para obtener que:
\(\boxed{X = -A^{3} = – \begin{pmatrix} 1 & -3/8 & -3/8\\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix} = \begin{pmatrix} -1 & 3/8 & 3/8\\ 0 & -1 & 0 \\ 0 & 0 & -1\end{pmatrix}}\)
Ejercicio 6

Apartado a)
Expresando el sistema en forma de matriz ampliada:
\(A^{*} = \left [ \begin{array}{ccc|c} 0 & 1 & 1 & 1 \\ (k-1) & 1 & 1 & k \\ 1 & (k-1) & 1 & 0 \end{array} \right ]\)
Si el determinante de la matriz del sistema es distinto de 0, entonces el sistema es compatible determinado. Si es nulo, el sistema es compatible indeterminado o incompatible. Para ver con qué valores de \(k\) se da cada caso, primero vamos a obtener el determinante.
\(|A| = \begin{vmatrix} 0 & 1 & 1 \\ (k-1) & 1 & 1 \\ 1 & (k-1) & 1 \end{vmatrix} = k^{2} – 3k + 2\)
Resolviendo la ecuación de segundo grado (\(k^{2} – 3k + 2 = 0\)), el determinante se anula para \(k = 1\) y \(k=2\). Por lo tanto, para \(k \neq 1,2\) el sistema es compatible determinado.
Para \(k=2\) la matriz ampliada queda:
\(A^{*} = \left [ \begin{array}{ccc|c} 0 & 1 & 1 & 1 \\ 1 & 1 & 1 & 2 \\ 1 & 1 & 1 & 0 \end{array} \right ]\)
Ya se podría deducir que el sistema es incompatible viendo las 2 últimas filas, pero para comprobarlo calculamos el rango de la matriz ampliada, sustituyendo por ejemplo la tercera columna:
\(|A^{*}| = \begin{vmatrix} 0 & 1 & 1 \\ 1 & 1 & 2 \\ 1 & 1 & 0 \end{vmatrix} = 2 \neq 0\)
Por lo tanto, como \(rang(A) = 2 < rang(A^{*}) = 3\), confirmamos que para \(k=2\) el sistema es incompatible.
Para \(k=1\) la matriz ampliada queda:
\(A^{*} = \left [ \begin{array}{ccc|c} 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 0 \end{array} \right ]\)
Observamos que tenemos 2 columnas idénticas (segunda y cuarta), por lo que el rango de la matriz ampliada va a seguir siendo 2 igual que el de la matriz del sistema. Por lo tanto, para \(k=1\) el sistema es compatible indeterminado.
Recapitulando:
- Para \(k \neq 1,2\) el sistema es compatible determinado.
- Para \(k=2\) el sistema es incompatible.
- Para \(k=1\) el sistema es compatible indeterminado.
Apartado b)
Tenemos que resolver para \(k=1\), que sabemos que el sistema es compatible indeterminado, teniendo infinitas soluciones. Eso implica que hay una fila de ecuaciones redundante (ya que es combinación lineal de las otras 2). Viendo la matriz ampliada nos damos cuenta que tanto la primera como la segunda fila son idénticas. Eliminamos una de ellas y el sistema nos queda:
\(\left\{\begin{matrix}y+z=1\\x+z=0\end{matrix}\right .\)Tomando por ejemplo \(z\) como variable paramétrica, nos queda que:
\(\left\{\begin{array}{ccc}x &=& – \lambda \\y &=& 1 – \lambda \\ z &=& \lambda \end{array}\right .\)La solución \(y = 0\) se da haciendo \(\lambda = 1\):
\(\boxed{\left\{\begin{matrix}x = – 1 \\y = 0 \\ z = 1 \end{matrix}\right .}\)Ejercicio 7

Apartado a)
En primer lugar escribimos la recta en forma paramétrica, que sería similar a resolver un sistema compatible indeterminado como en el ejercicio anterior. En este caso haré \(y = \lambda\):
\(\left\{\begin{array}{ccc}x &= &3 + \lambda \\y &=& \lambda \\ z &=& -1 + \lambda \end{array}\right .\)Esto quiere decir que la recta pasa por el punto \((3,0,-1)\) y tiene como vector el \((1,1,1)\).
Para obtener el punto simétrico con respecto a la recta, primero generaremos un plano perpendicular a la recta y que pase por el punto \(P\), obtendremos el punto de intersección entre recta y plano \(M\), y con el vector \(\vec{PM}\) obtendremos el \(\vec{MP’}\) para obtener finalmente el punto simétrico \(P’\). A continuación pongo una imagen del esquema para que se entienda mejor el procedimiento:
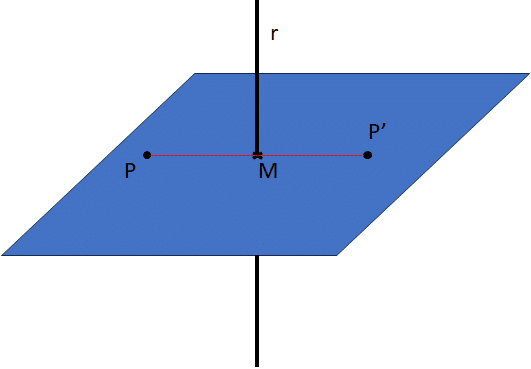
La ecuación del plano tiene la forma \(Ax + By + Cz + D\), donde \(A,B,C\) son los componentes del vector normal al plano (que, en nuestro caso ya lo tenemos porque es el de la recta), y \(D\) es una constante que estipula a qué altura de la recta se ubica el plano. Para determinarlo introduciremos las coordenadas del punto \(P\) en la ecuación del plano de forma que la constante debe cumplir que dicho punto está contenido en el plano.
\( \sigma : x + y + z + D = 0 \)
\( \sigma : 2 + 2 + 1 + D = 0 \iff D = -5 \)
La ecuación del plano es por lo tanto:
\( \sigma : x + y + z -5 = 0 \)
Ahora necesitamos saber dónde se encuentra el punto \(M\). Para ello, sustituimos las ecuaciones paramétricas de la recta en la ecuación del plano:
\( \sigma : (3+\lambda) + \lambda + (-1+\lambda) -5 = 0 \iff \lambda = 1 \)
Por lo tanto, el punto \(M\) es el \(M(4,1,0)\).
Como \(M\) se encuentra espacialmente a mitad entre \(P\) y \(P’\):
\(M = \dfrac{P + P’}{2} \rightarrow \boxed{P’ = 2M – P = (8,2,0) – (2,2,1) = (6,0,-1)}\)
Apartado b)
Para resolver este apartado la idea es la misma. En primer lugar se obtiene la recta perpendicular al plano que pasa por el punto \(Q\). Se obtiene la intersección de la recta con el plano (punto \(M\)). Finalmente se obtiene el punto simétrico \(Q’\) extendiendo el vector \(\vec{QM}\).
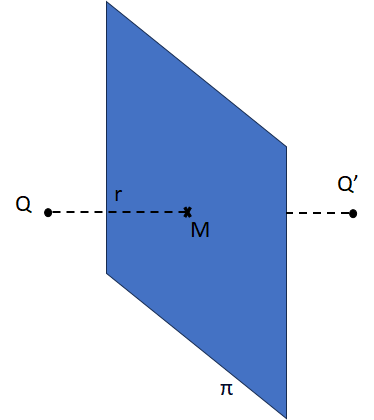
De la ecuación del plano sabemos que el vector de la recta es el \((1,-2,1)\). Además, como pasa por el punto \(Q\), podemos escribir paramétricamente la recta como:
\(\left\{\begin{array}{ccc}x &=& 1+ \lambda \\y &=& -1 – 2\lambda \\ z &=& -3 + \lambda \end{array}\right .\)Para obtener el punto de intersección introducimos las ecuaciones de la recta en el plano:
\((1+ \lambda) -2 (-1-2 \lambda) + (-3 + \lambda) + 6 = 0 \iff \lambda = -1\)
El punto \(M\) resulta por lo tanto el \(M(0,1,-4)\). Por lo tanto:
\(M = \dfrac{Q’-Q}{2} \rightarrow \boxed{Q’ = 2M – Q = (0,2,-8) – (1,-1,-3) = (-1,3,-5)}\)
Ejercicio 8

Apartado a)
Las rectas pueden ser paralelas, coincidentes, cortarse y cruzarse.
- Paralelas: Tienen vectores proporcionales.
- Coincidentes: Además de ser paralelas, todos sus puntos coinciden.
- Rectas que se cruzan: Sus vectores no son proporcionales, y no tienen ningún punto en común.
- Rectas que se cortan: Se cruzan e intersecan en un único punto. Pueden ser perpendiculares (producto escalar de vectores es nulo) o secantes.
Para empezar vamos a poner las rectas en forma paramétrica para identificar sus vectores.
\(r :\left\{\begin{array}{ccc}x &=& \lambda \\y &=& 0 \\ z &=& 2\lambda \end{array}\right . \rightarrow \left\{\begin{array}{ccc}P_{r} &=& (0,0,0) \\v_{r} &=& (1,0,2) \end{array}\right .\) \(s :\left\{\begin{array}{ccc}x &=& \lambda \\y &=& -7 – \lambda \\ z &=& 0 \end{array}\right . \rightarrow \left\{\begin{array}{ccc}P_{s} &=& (0,-7,0) \\v_{s} &=& (1,-1,0) \end{array}\right .\)Observamos que sus vectores no son proporcionales, por lo tanto no son ni paralelas ni coincidentes. Si las rectas se cortan, ambas deben pertenecer a un mismo plano. Para comprobar si son coplanarias, podemos calcular un triple producto escalar. Si el resultado es nulo, entonces se cortan. Si no, se cruzan.
Vamos a emplear los vectores de cada recta y un vector que una dos puntos cualesquiera de las rectas, como por ejemplo el \(\vec{P_{r}P_{s}} = (0,-7,0)\). El triple producto escalar nos queda:
\(\boxed{\vec{P_{r}P_{s}} \cdot (\vec{v_{r}} \times \vec{v_{s}}) = \begin{vmatrix} 0 & -7 & 0 \\ 1 & 0 & 2 \\ 1 & -1 & 0 \end{vmatrix} = -14 \neq 0}\)
Por lo tanto, las rectas se cruzan pero no se cortan.
Apartado b)
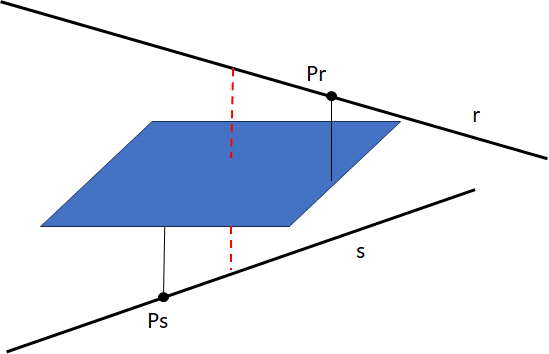
La ecuación del plano paralelo a ambas rectas viene dado por una normal que es el vector perpendicular a ambas rectas. Haciendo el producto vectorial:
\(\vec{v_{\pi}} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ 1 & 0 & 2 \\ 1 & -1 & 0 \end{vmatrix} = (2, 2, -1) \)El plano vendría dado por la ecuación \(2x + 2y – z + D = 0\). Tenemos ahora que determinar \(D\) para situar el plano equidistante de las rectas. Como las rectas son paralelas al plano, cualquier punto de cada una de las rectas se encuentra a la misma distancia del plano. Tomando por ejemplo los puntos que hemos definido como origen de las rectas en forma paramétricas, se debe cumplir:
\(d(P_{r},\pi) = d(P_{s},\pi)\)
Para obtener la distancia de la recta \(r\) al plano \(\pi\), generamos una recta que parta del punto \(P_{r}\) con vector el normal del plano:
\(r :\left\{\begin{array}{ccc}x &=& 2\lambda \\y &=& 2 \lambda \\ z &=& -\lambda \end{array}\right . \)El punto de corte será aquel que cumpla la ecuación del plano:
\(4 \lambda + 4 \lambda + \lambda + D = 0 \rightarrow \lambda = -\dfrac{D}{9}\)
El punto resultaría el \(M_{1} = \left (- \dfrac{2D}{9}, – \dfrac{2D}{9}, \dfrac{D}{9} \right )\)
Por lo tanto, la distancia de la recta \(r\) al plano \(\pi\) es:
\(d(P_{r},\pi) = \dfrac{D}{9} \sqrt{(-2-0)^{2} + (-2-0)^{2} + (1-0)^{2}} = \left|\dfrac{D}{3}\right |\)
Repetimos el mismo procedimiento con la recta \(s\)
\(r :\left\{\begin{array}{ccc}x &=& 2\lambda \\y &=& -7 + 2 \lambda \\ z &=& -\lambda \end{array}\right . \)El punto de corte será aquel que cumpla la ecuación del plano:
\(4 \lambda + -14 + 4 \lambda + \lambda + D = 0 \rightarrow \lambda = \dfrac{14-D}{9}\)
El punto resultaría el:
El punto resultaría el \(M_{2} = \left (\dfrac{28-2D}{9}, -7 + \dfrac{28-2D}{9}, \dfrac{14 – D}{9} \right )\)
Por lo tanto, la distancia de la recta \(s\) al plano \(\pi\) es:
\(d(P_{s},\pi) =\sqrt{\left(\dfrac{28-2D}{9} \right)^{2} + \left(\dfrac{28-2D}{9} \right)^{2} + \left(\dfrac{14 – D}{9} \right)^{2}} =\)
\(= \dfrac{14-D}{9} \sqrt{2^{2} + 2^{2} + 1} =\left |\dfrac{14-D}{3}\right |\)
Se debe de cumplir que las distancias sean las mismas, por lo tanto:
\(d(P_{r},\pi) = d(P_{s},\pi) \iff \left |\dfrac{D}{3}\right | =\left |\dfrac{14-D}{3}\right | \iff \boxed{D= 7}\).
Siendo la ecuación del plano equidistante:
\(\boxed{\pi : 2x + 2y – z + 7 = 0} \)

![Examen Matemáticas Andalucía Junio 2023 Resuelto Selectividad [PEvAU] MatematicasII_1](https://ingenieriabasica.es/wp-content/uploads/2023/07/MatematicasII_1-143x200.jpg)

¡Impresionante, muchas gracias por tu ayuda y por compartir tu pasión por las ciencias!
Estaré atento de más publicaciones