Esta es una de las preguntas que TODO el mundo se ha hecho alguna vez. ¿Cómo es posible que siempre caigan de pie los gatos?
En principio se piensa que es debido a alguna característica geométrica o a que simplemente son capaces de girarse muy rápido debido a su agilidad. Y es que, dentro de la inherente dificultad para girar tan rápido durante la caída entra en juego un término físico inviolable: La conservación del momento angular.
Vale, digamos que el gato es muy hábil y es capaz de girarse muy rápido y caer perfecto como lo haría un saltador olímpico.
Pues no, porque si el gato cae con momento angular nulo, no puede girarse 180ª simplemente girando la columna porque se estaría creando momento de la nada (La variación del momento angular es igual al momento que crean las fuerzas externas).
Bueno… pues entonces el gato se “impulsa” con el aire, generando ese momento externo que le permite girar.
Vale, en el caso de un fluido como el agua sí. Si estamos nadando y queremos girar sólo tenemos que hacer un movimiento con los brazos para empujar agua y podremos girar sobre nosotros mismos. Pero porque el agua es mucho más denso que el aire y nos da esa capacidad propulsiva. El aire, a menos que tengamos la herramienta apropiada (Un ala u otra cosa de gran superficie) no nos aportará ningún empuje.
¿Entonces qué? Una vez descartadas todas estas cosas tenemos algo claro; El momento angular se mantiene constante en todo momento en lo que sería el cuerpo completo del gato. Sin embargo, que se mantenga constante no implica que no haya rotaciones relativas.
Helicópteros
¿Nunca os habéis preguntado por qué un helicóptero tiene 2 hélices? La principal es obvio; para poder volar. Pero, ¿Y la trasera?
Si habéis jugado al mítico GTA IV lo habréis experimentado vosotros mismos; al romperse la hélice trasera el helicóptero comienza a girar sobre sí mismo.
Esto se debe porque, al igual que ocurre con los gatos y cualquier otro cuerpo físico, el momento angular se conserva. De esta forma, al girar la hélice en sentido antihorario, se induce un giro horario en el cuerpo del helicóptero. Es la hélice trasera la que, por medio del empuje del aire, genera esa fuerza externa que induce un momento capaz de contrarrestar esta rotación. Si esta hélice trasera se rompe, el helicóptero se descontrola


Helicópteros con 2 hélices que giran en sentido contrario y anulan el momento angular, de manera que no es necesario rotor de cola
Una vez introducido esto, obtenemos una pista: El gato puede rotar la parte inferior y superior de manera que el momento angular total se mantiene constante.
El momento cinético
Cuando un sólido rígido se encuentra rotando podemos hacer una analogía con un cuerpo de masa m que se mantiene en un movimiento rectilíneo uniforme.
Siguiendo la primera ley de newton o ley de inercia, si sobre un cuerpo no actúan fuerzas, este permanecerá indefinidamente moviéndose en movimiento rectilíneo uniforme (incluyendo el estado de reposo, que equivale a velocidad cero).
Lo mismo ocurre con el momento cinético. Para un cuerpo rotando sin ausencia de fuerzas se tiene que:
\( \dfrac{d\vec{L}}{dt} = \dfrac{d}{dt}\{[I]*\vec{w}\}=0\)
Siendo \([I]\) la matriz del momento cinético. Si el eje de giro es un eje principal, podemos escribir directamente:
\( \dfrac{d\vec{L}}{dt} = \dfrac{d}{dt}\{I*w\}=0\)
De lo cual extraemos que, en ausencia de fuerzas, \( L_{0}=I*w=cte\). De esta forma, existe una relación inversamente proporcional entre el momento de inercia de un cuerpo y la velocidad a la que gira.
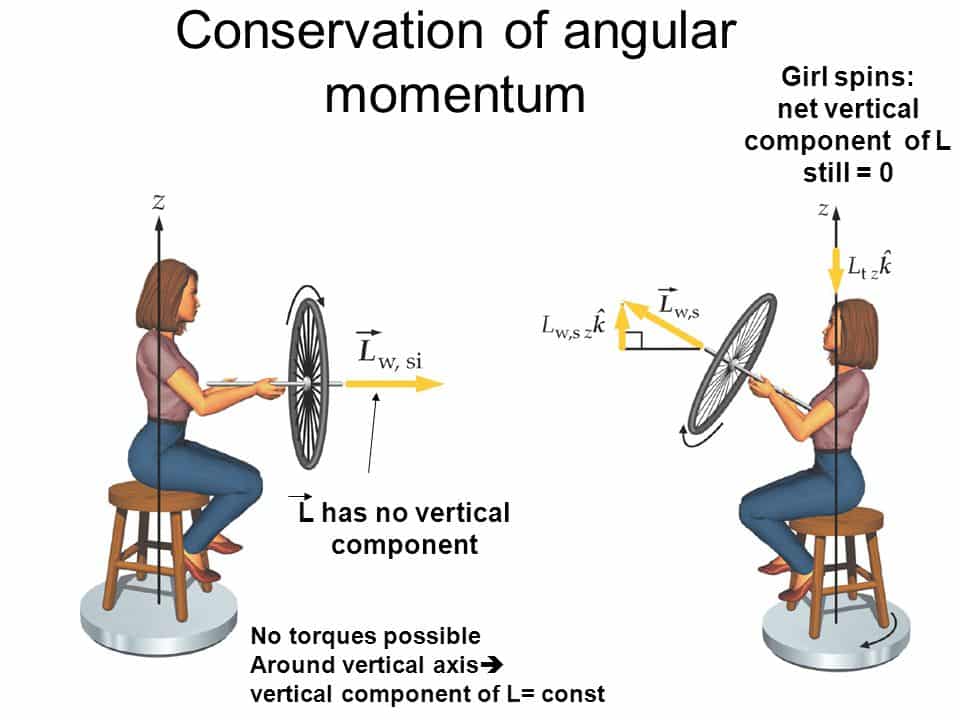
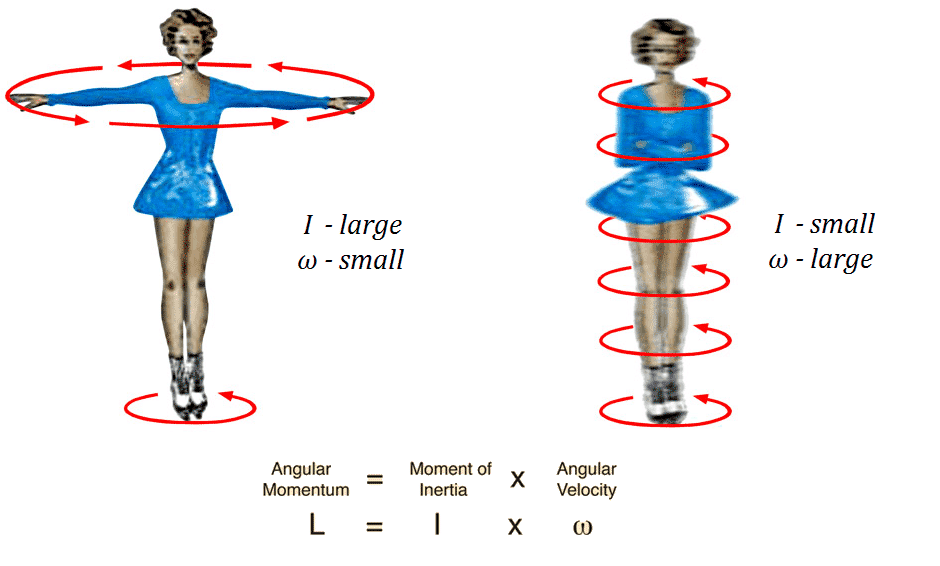
La relación se observa claramente en el caso de los patinadores de hielo que son capaces de alterar la velocidad de giro. ¿Cómo lo hacen?

Si extendemos los brazos aumenta la inercia. Por lo tanto, disminuye la velocidad de giro. Y ocurre lo mismo al revés
Gato que cae sin giro inicial
Si sostenemos un gato boca abajo y lo dejamos caer, en todo momento el momento angular es nulo ya que inicialmente lo era. Por lo tanto se tiene que nuestra constante es \(I*w=0\)
Como hemos introducido anteriormente, el truco del gato es dividir su cuerpo en 2 partes que giran alrededor del mismo eje: \(I=I_{sup}+I_{inf}\). Nuestro momento lineal total queda:
\(I_{sup}*w _{sup} + I_{inf}*w _{inf} =0\)
Una vez hecha esta división, sólo nos hace falta explicar el movimiento del gato.
Algoritmo de caída del gato
Al gato no le interesa ni las fuerzas, ni la inercia ni la velocidad. Lo que le interesa es girar 180º y caer de pie. Por lo tanto, lo que necesita es de alguna inducir giros jugando con la relación entre inercia – velocidad de giro de manera que al final caiga de pie.
Lo que primero tiende a hacer es a colocar la parte superior (Cabeza y patas delanteras) en la posición adecuada. ¿Y cómo lo hace sin descontrolar el giro? Aumentando la inercia de las patas traseras y cola \((\uparrow I _{inf})\) , y disminuyendo la inercia de las patas delanteras \((\downarrow I _{sup})\) . De esta forma, como \(I_{sup}*w _{sup} + I_{inf}*w _{inf} =0\) , con un pequeño giro de la parte trasera \((\downarrow w _{inf})\) es capaz de girar completamente la parte delantera \((\uparrow w _{sup})\) . La relación entre el giro de la parte delantera y trasera es:
\(w_{sup}=-\dfrac{ I_{inf} }{ I_{sup} } \cdot w _{inf} \)
Es decir, en valor absoluto mayor y con sentido opuesto.
Una vez la parte delantera se encuentra en una posición apropiada, hace falta el movimiento inverso. El gato extiende las extremidades delanteras \((\uparrow I _{sup})\) y encoge las traseras \((\downarrow I _{inf})\) , y mediante un pequeño giro de la parte delantera es capaz de girar completamente la parte trasera.

Un punto clave en los movimientos del gato es el arqueo de su columna. No sólo extiende las extremidades, sino que al arquear la espalda varía la dirección de rotación y así manipula aún más a su favor el giro. Todo esto, junto con la cola, permite que el gato caiga de pie y que deje de rotar cuando se encuentra en la posición idónea, cumpliéndose nuestra condición de que \(I*w=0\) en todo momento.
Aquí os dejo un vídeo de unos gatos intentando caer en «gravedad cero» (Ingravidez). Por lo visto pierden completamente la orientación
Tostadas que giran solas
En el caso del gato todo ha quedado claro; mueve partes de su cuerpo de forma oportuna para girar de la forma que quiere. Pero, ¿Cómo lo hacen las tostadas? ¿Acaso tienen vida propia y no nos hemos dado cuenta?
Con las tostadas ocurre algo muy peculiar, y es que se combina ciencia con superstición. Y es que, sí, debido al desplazamiento del centro de gravedad podemos decir que tiende a caer sobre una cara. Sin embargo, esta tendencia al giro es despreciable.
Desplazamiento centro de gravedad
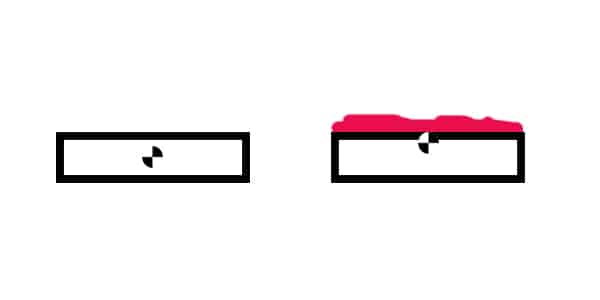
A la derecha, tostada con mermelada. Su centro de gravedad sube hacia arriba.
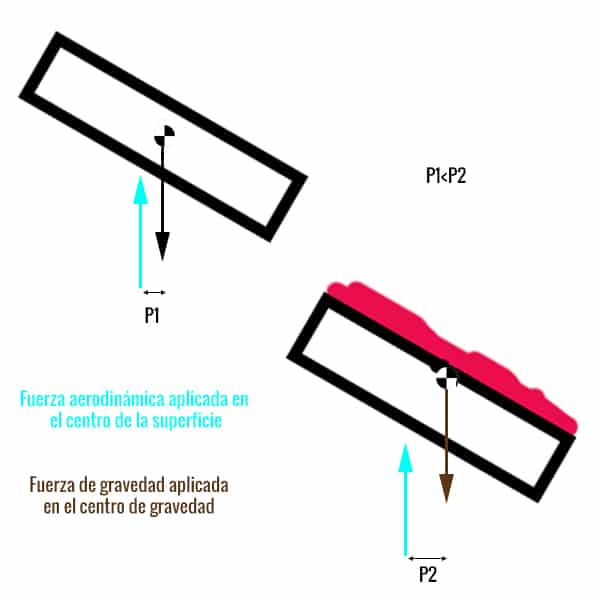
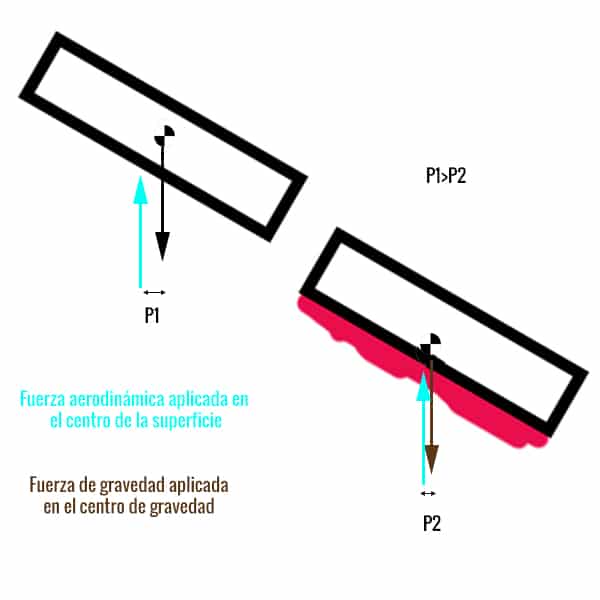
Observamos que el desplazamiento del centro de gravedad respecto al centro geométrico produce un equilibrio inestable en caso de caer boca arriba, y que el par de fuerzas induce un giro que tiende a hacerla caer boca abajo. Sin embargo, haciendo unas cuentas rápidas nos damos cuenta de que el momento inducido es muy pequeño en comparación con la inercia de la tostada.
El orden de magnitud de la inercia es de \(ML^{2}\), mientras que el orden de magnitud del par es de \(M*L*d\). Al ser L (Longitud lado de tostada) mucho mayor que la distancia d de aplicación de las fuerzas que genera el par, en una caída pequeña de varios metros es despreciable.
Entonces, ¿Por qué ocurre?
Esto se debe a la altura de caída. Cuando una tostada sobresale demasiado del borde de la mesa, el peso hace que gire y caiga al suelo.

Lo que ocurre es que la velocidad de giro es tal que a esa altura media sólo permite dar una vuelta. Por lo tanto, tiende a caer sobre dicha cara.
Haced una prueba no con una tostada, sino con cualquier otro objeto similar. Por ejemplo, una cartera cerrada con una parte llena de monedas o una libreta a la que le enganchéis un peso a una de las tapas.
Al dejarlo caer de esta forma generalmente sólo dará una vuelta independientemente de qué cara pongamos boca arriba inicialmente. Lo que ocurre es que la tostada SIEMPRE se encuentra boca arriba en el plato y por lo tanto al girar cae boca abajo.
Aún así nuestra percepción de la caída de la tostada boca abajo tiene un factor psicológico. Si la tostada cae boca arriba todo bien. ¡Qué suerte! La recogemos y punto. Sin embargo, si cae boca abajo… MIERDA, ahora me toca limpiarlo…. Nos llama mucho más la atención y nos refuerza la idea de que las tostadas siempre caen boca abajo.
Dicho esto, se supone que si lanzamos una tostada con una posición y velocidad angular aleatoria desde una altura suficientemente alta, el porcentaje de boca arriba – boca abajo debería de ser cercano al 50% (En teoría un poco mayor en el caso de las caídas boca abajo debido al desplazamiento del centro de gravedad como hemos demostrado). Y de hecho, hicieron un experimento y ocurrió así.
¿Qué ocurre si pegamos una tostada a un gato?
Este es un caso especial en la caída de objetos y lleva intrigando a la física durante años. Para comprobar qué ocurriría hicieron una prueba pegando una tostada en la espalda de un gato. Te sorprenderá el resultado.




Wow muy interesante
Si tiras un gato muy bajo no cae de pie