¡Muy buenas a todos! Esta es mi primera entrada en el blog, titulada «Tiro parabólico – Estudio cualitativo de la máxima distancia horizontal»
Introducción
Vamos a estudiar el «Tiro parabólico», deduciendo matemáticamente las expresiones o fórmulas desde 0 y haremos un estudio cualitativo de cómo el ángulo de lanzamiento afecta a la distancia horizontal. Esta distancia horizontal es la que realmente nos interesa del tiro debido a su utilidad (Lanzamiento de jabalina, golf, béisbol, arco…).
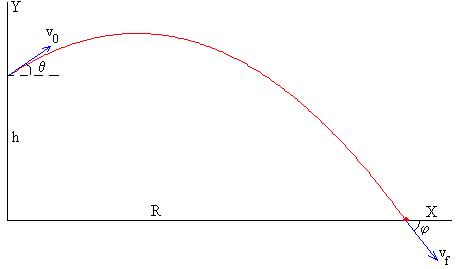
- La máxima distancia vertical como es obvio se obtiene a un ángulo de π/2 a cualquier vo y h
Nos encontramos ante un problema del tipo «Tiro parabólico». Nuestros únicos datos son la altura a la que se lanza el objeto, h, y la velocidad inicial que se le imprime a dicho cuerpo, vo. La masa del cuerpo es m, aunque como sabemos no influye en el tiro. El ángulo de lanzamiento se llamará θ y es variable. Además, la única fuerza presente es la fuerza gravitatoria, que se simplifica a m*g
Podríamos hallar las ecuaciones del movimiento de un sistema complejo empleando la mecánica analítica. Sin embargo, debido a la simplicidad del problema emplearemos la Segunda Ley de Newton (Mecánica clásica) y hallaremos la ecuación del movimiento en función del tiempo
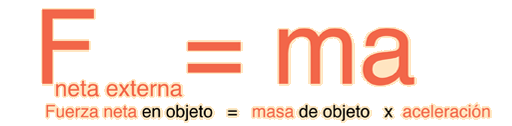
Cálculo de velocidad
Primero hallamos la velocidad. Sabemos que la única aceleración que afecta a la masa es la de la gravedad, y que se corresponde con la derivada de la velocidad respecto al tiempo. Integrando obtenemos:
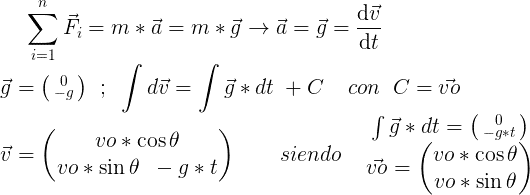
Cálculo de posición
Luego hallamos la ecuación del movimiento (Ley horaria) empleando el mismo método. Una vez obtenida la velocidad, al ser el vector posición la derivada de la velocidad respecto al tiempo integramos de nuevo:
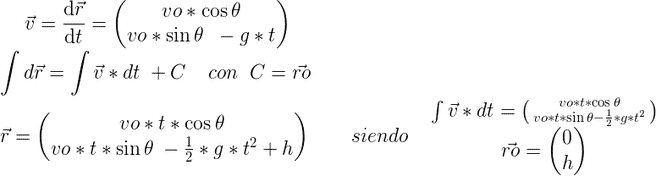
Ya tenemos definida por completo la trayectoria que va a seguir la masa. Los valores de vo, h y g son conocidos (constantes), mientras que t y θ son variables.
Distancia recorrida en función del ángulo
Recordemos qué es lo que queremos obtener; el ángulo mediante el cuál la distancia recorrida sobre el eje x, es decir, xf sea máxima. Por lo tanto, tendríamos una función f(t,θ)= vo*t*cos(θ) que queremos hacer máxima. Esto se dará en los valores más altos de t y en los valores más altos de cos(θ)
Sin embargo, el tiempo no es una variable que tenemos que hacer máxima. El tiempo t tiene un valor fijo, que es el tiempo en el que la masa toca el suelo. ¿Cómo podemos obtener dicho valor? De la ecuación del movimiento cuando y=0
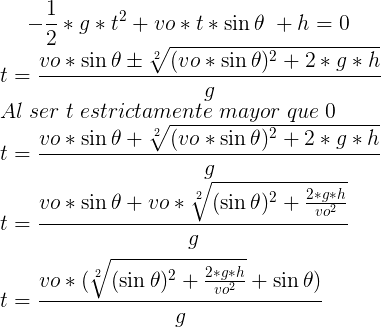
Si introducimos el valor de t en la ecuación de x, se nos queda una función que dado unos valores iniciales de vo y h depende exclusivamente de θ que nos indica la distancia horizontal en función del ángulo de lanzamiento.
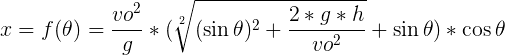
Analíticamente el valor de θ se obtendría derivando e igualando a 0. Consiste en un problema de búsqueda de máximos acotando los valores de θ entre [0,π/2] ya que no nos interesan distancias negativas. Sin embargo, supone un cálculo complicado al no aparecer explícitamente el valor del ángulo y este depender de los parámetros iniciales vo y h.
Por ello, una solución alternativa mucho más intuitiva y sencilla es analizar gráficamente los valores de dicha función. Para ello, tomamos un sistema cartesianos de ejes x e y, tal que y=f(θ) y x=θ. Vamos a analizar los valores del ángulo que hacen máxima la distancia recorrida.
Las imágenes siguientes muestran la distancia recorrida(Eje ordenadas) en función del ángulo (Eje coordenadas). No confundir con la ecuación de la trayectoria. El punto marcado indica el máximo de la gráfica
Gráficos generados empleando la web Desmos.com
SOLUCIONES PARA DIFERENTES VALORES
–Cuando h=0
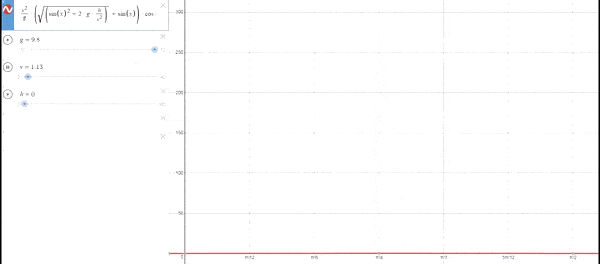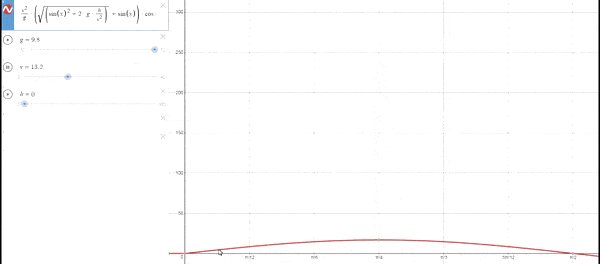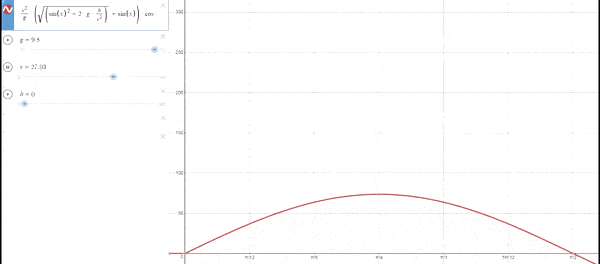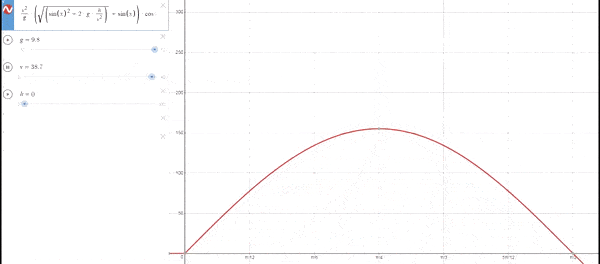
La máxima distancia se alcanza con un ángulo de 45º independientemente de la velocidad de lanzamiento. Esto se debe a que se compensa
–Cuando h es variable para una vo fija
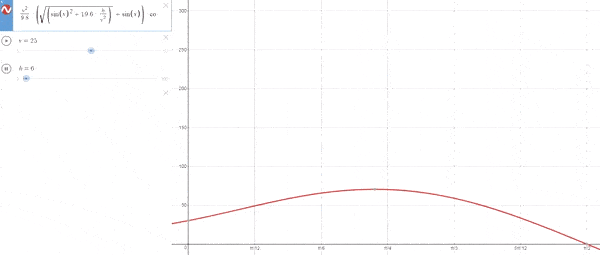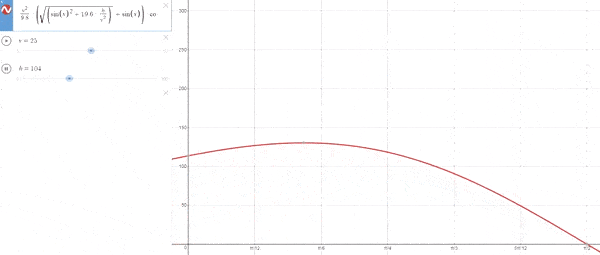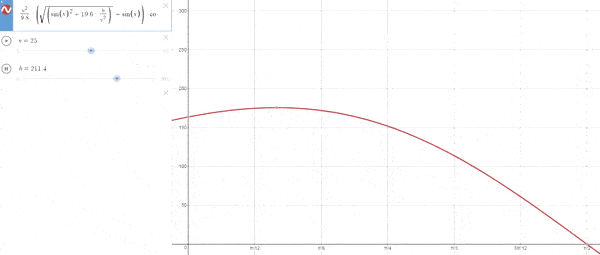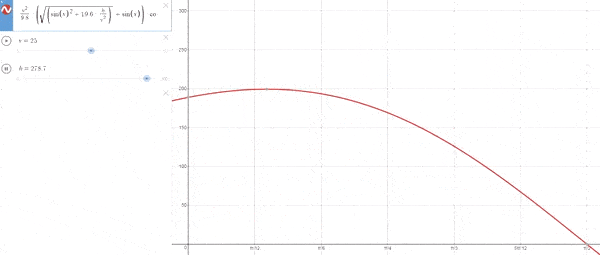
Empezando con h=0 el ángulo es 45º y a medida que aumenta la altura, el ángulo cada vez es menor.[La explicación lógica es que a grandes alturas no hace tanta falta aumentar el ángulo de lanzamiento para ganar altura como el tener un menor ángulo para desplazarse más rápidamente horizontalmente]
–Cuando h es fija para una vo variable
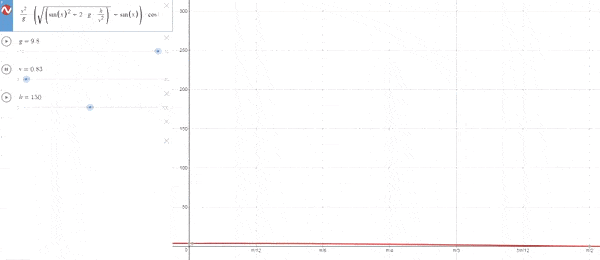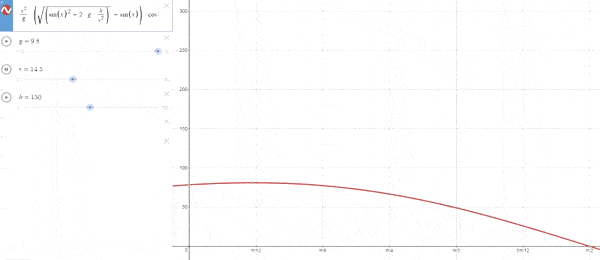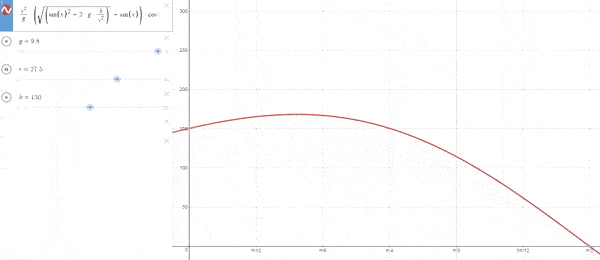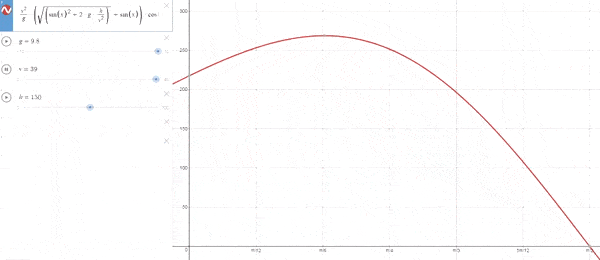
*Caso particular vo=o*
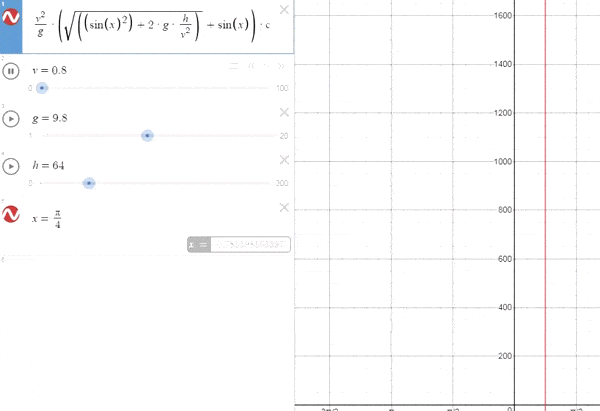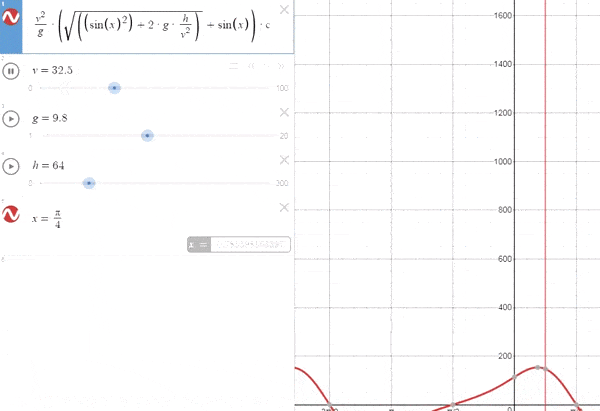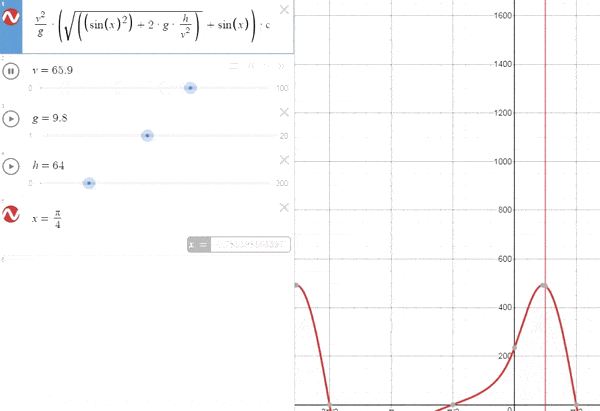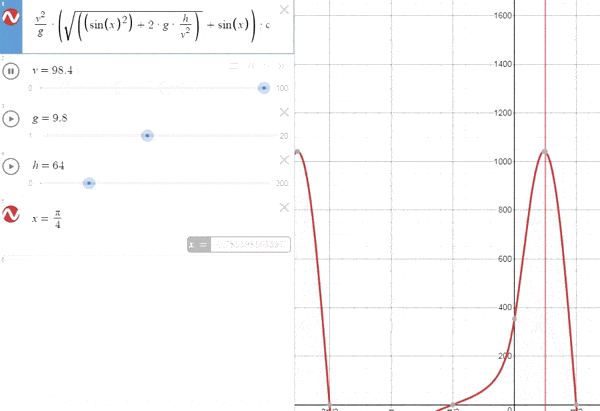
*Observamos que para vo=0 no hay movimiento, lógico*
A medida que aumenta el valor de la velocidad aumenta la inclinación, llegando a un valor máximo de 45º cuando la velocidad es muy alta.[La explicación lógica es que a pequeñas velocidades el tiempo de vuelo es pequeño, y como tal se priorizan ángulos pequeños para aumentar la distancia recorrida. Con una velocidad alta, el tiempo de vuelo va a ser mayor por lo que para hacer frente a la aceleración se necesitará coger mayor altura en las primeras fases del vuelo.
EXTRA: ¿Cómo sera el tiro parabólico en otro planeta?
–Variando g con h=0 y vo fija
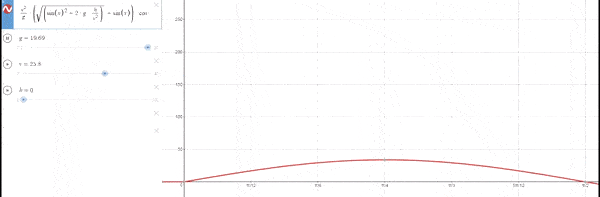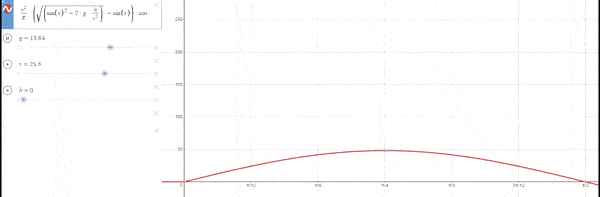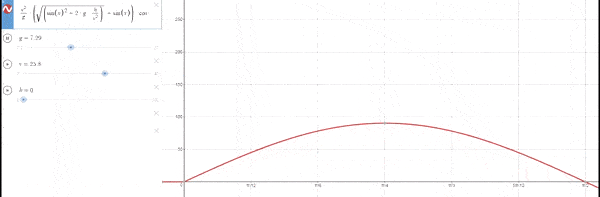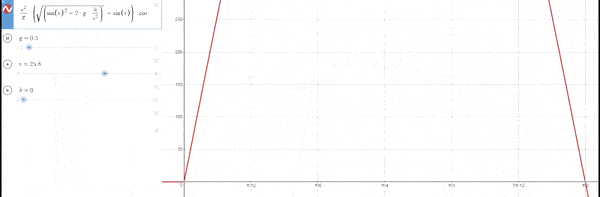
El ángulo en el cual se obtiene el máximo desplazamiento es 45º independientemente de la gravedad
–Variando g con h distinta de 0 y vo fija
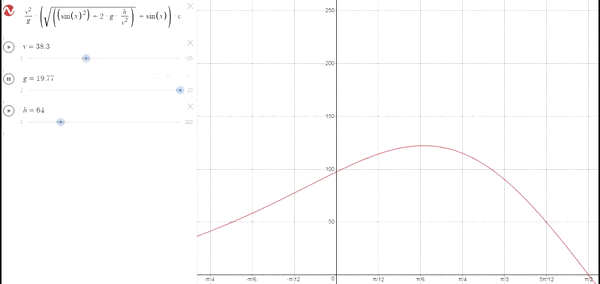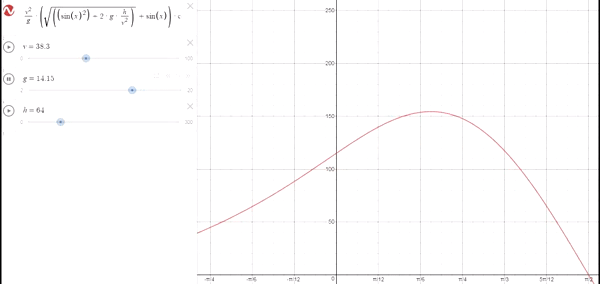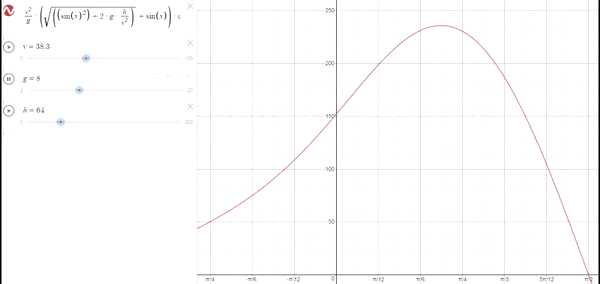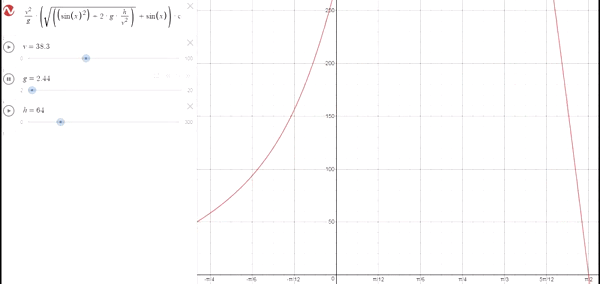
Ocurre similar a cuando aumentamos la velocidad a una altura constante distinta de 0. A medida que disminuye la gravedad, el ángulo optimo va aumentando hasta tocar con 45º
*Caso especial g=0*
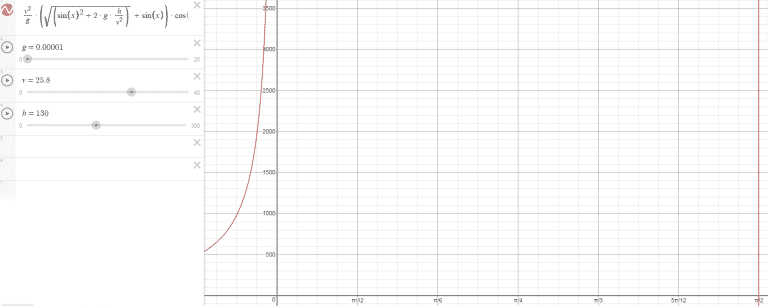
Como es lógico, cuando g tiende a 0 a cualquier ángulo de lanzamiento (0,π/2)((Intervalo abierto)) es máximo puesto que nunca cae.
Si has llegado a este punto te agradezco enormemente haber leído el artículo y pido disculpas por haberlo hecho «demasiado matemático», distinto al tipo de artículos que hago últimamente. Si te ha gustado, tengo dos artículos similares:


1 comentario en «Tiro parabólico – Estudio cualitativo de la máxima distancia horizontal»