Supongamos que tenemos una calculadora como la de la imagen. Es decir, con el típico teclado numérico en el que los números distintos al 0 se encuentran en una cuadrícula 3×3.
Pues dicha distribución tiene una propiedad muy interesante: Si generas un número de 4 dígitos siguiendo un patrón rectangular, dicho número es múltiplo de 11.
Pongamos el siguiente ejemplo:
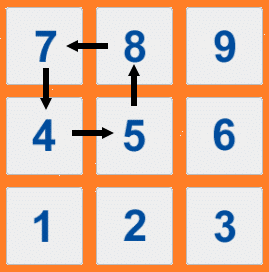
7458/11 = 678
4587/11 = 417
5874/11 = 534
8745/11 = 795
Sorprendente, ¿no? Pues es aún más sorprendente si pensamos en rectángulos e incluso rectángulos degenerados, por ejemplo:
7964/11 = 724
2893/11 = 263
1221/11 = 111
3993/11 = 363
Pero… ¿Cómo es posible esto?
Como siempre, vamos a exponer la demostración matemática
Demostración matemática
Para empezar, una de las condiciones que hemos puesto es que sea un número de 4 dígitos. Por lo tanto, siendo a, b, c, d los dígitos empleados, dicho número puede expresarse en base \(l\) como:
\(abcd = a \cdot l^{3} + b \cdot l^{2} + c \cdot l + d\)
Teniendo en cuenta que \(0 < a, b, c, d < l\)
Y queremos comprobar su divisibilidad con respecto al 11, que en base \(l\) es: \(11 = l + 1\)
Por otra parte, algunas combinaciones son divisibles entre \(l + 1\):
\(l^{3} + 1 = (l+1) \cdot (l^{2} – l + 1)\)
\(l^{2} -1 = (l+1) \cdot (l-1)\)
Por lo tanto, podemos escribir nuestro número como:
\(\displaystyle abcd = a \cdot l^{3} + b \cdot l^{2} + c \cdot l + d = a (l^{3} + 1) + b(l^{2} -1) + c (l+1) – (a-b+c-d) =\)
\(\displaystyle = (l+1) \cdot (a (l^{2} – l + 1) + b (l-1) + c) + ((b+d)-(a+c))\)
Por lo tanto, si dividimos todo ese bloque entre \(11 = l + 1\), quedaría:
\(\dfrac{abcd}{11} = (a (l^{2} – l + 1) + b (l-1) + c) + \dfrac{(b+d)-(a+c)}{11}\)
Lo cual resulta un número entero \(\iff (b+d)-(a+c)\) es 0 o múltiplo de 11.
Y dicho resultado se cumple en el típico teclado 3×3, en el que la suma de los números de las dos esquinas opuestas del rectángulo da como resultado el mismo número que la suma de las otras dos esquinas opuestas.