¡Muy buenas a todos! En esta entrada, como habréis adivinado por el título, voy a presentar una serie de acertijos matemáticos nivel medio-alto para poner a prueba a mis lectores.
La dinámica va a ser la siguiente: propondré 7 acertijos pero no pondré la solución. Voy a dejar que vosotros seáis los que los resolváis, y para ello tendréis que poner un comentario con la solución y una breve explicación de cómo habéis llegado a ella. Voy a ordenarlos de menos a más difícil para hacerlo más emocionante. Una vez hayáis resuelto el acertijo, editaré la entrada añadiendo el desarrollo de la solución y pondré el nombre con el cual habéis publicado el comentario.
Cabe destacar que los comentarios del blog deben ser aprobados manualmente por mí (así evito el SPAM) pero los apruebo todos en menos de 24h sean buenos o malos, por lo que si no aparece vuestra respuesta esperad unas horas.
Además, dejaré un par de pistas en los comentarios por orden de acertijo para no haceros spoiler si no queríais ver nada. Por eso recomiendo empezar por el primer acertijo y si no lo sacáis ni con ayuda ir a por el siguiente.
Enunciados
Números agrupados
A continuación se presenta una serie de números:

El objetivo es agrupar los 9 números en 3 grupos de 3 números cada uno tal que el producto de los números de cada grupo valga lo mismo en todos los grupos.
Es posible hacer los grupos por prueba y error; no obstante, a ver si sois capaces de usar las matemáticas de manera inteligente para encontrar la solución
Juego de dados

Estás jugando en un casino a un juego de dados. Tienes 100€ en la cuenta. El juego consiste en que tiras una pareja de dados y:
- Si sale un 7,8 o 9 ganas 50€
- En caso contrario, pierdes 50€
Apuestas constantemente y el juego acaba cuando llegas a 200€ en la cuenta o acabas con 0€. La pregunta es… ¿Qué probabilidades tienes de salir ganador?
Áreas y semicírculos
En la siguiente figura se observa una semicircunferencia en la parte superior y un cuarto de circunferencia debajo:
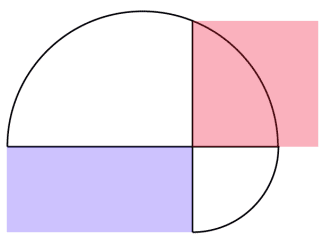
La pregunta es… ¿Qué tiene más área? ¿El cuadrado rojo o el rectángulo azul?
Carrera matemática

En una carrera de 100 metros, el corredor A llega a la meta cuando el corredor B se encuentra a 5 metros. Cuando el corredor B llega a la meta, el corredor C se encuentra a 10 metros.
Cuando el corredor A llegó a la meta… ¿A qué distancia estaba el corredor C?
Sumas bonitas
A continuación se presenta un ejemplo de suma:
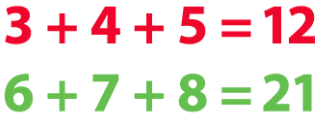
Es decir, 6 números consecutivos, tal que si sumamos los 3 primeros obtenemos un número de dos dígitos que es precisamente el reverso de la suma de los 3 últimos. La pregunta es… ¿Qué otras posibles secuencias de números cumplen dicha propiedad?
Borracho matemático

Tienes una botella de 10L de vino. El primer día bebes 1L de contenido y añades 1L de agua para volver a dejarla llena y la mezclas perfectamente. El segundo día bebes 2L de contenido y añades 2L de agua para volver a dejarla llena y la mezclas perfectamente. Haces esto cada día y el décimo día bebes los 10L de contenido.
Tras beber el décimo día… ¿Cuántos litros de agua has bebido?
Suma y resta cuadrática
Se presenta la siguiente operación matemática:
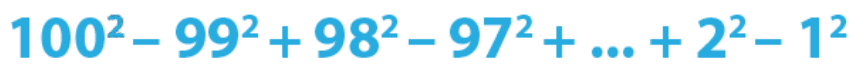
Obviamente sin hacer la operación completa… ¿Cuál es el resultado?
Soluciones
Números agrupados
Carlos Cajo ha encontrado la solución. La respuesta es:
(3,8,35)
(4,7,30)
(5,6,28)
El producto de todos los números es \(2^{9} \cdot 3^{3} \cdot 5^{3} \cdot 7^{3}\)
Es decir, que el producto de cada grupo debe ser \(2^{3} \cdot 3 \cdot 5 \cdot 7 = 840\)
Si, por ejemplo, dividimos \(840\) entre el número más grande \((35)\), nos da como resultado \(24 = 3 \cdot 8\). Es decir, que un grupo es (3,8,35).
Haciendo lo mismo para el número \(30\), obtenemos \(24 = 4 \cdot 7\). Es decir, que otro grupo es (4,7,30).
El último grupo sale por descarte y haciendo el mismo razonamiento: (5,6,28)
Juego de dados
Jose ha dado con la solución:
Tenemos 2 dados de 6 caras cada uno, por lo que hay 36 posibles combinaciones. La probabilidad de sacar cada uno de los números es:
- 2: 1 y 1 -> 1
- 3: 1 y 2, 2 y 1 -> 2
- 4: 1 y 3, 3 y 1, 2 y 2 -> 3
- 5: … -> 4
- 6: …-> 5
- 7: …-> 6
- 8: …-> 5
- 9: …-> 4
- 10: 4 y 6, 6 y 4, 5 y 5 -> 3
- 11: 6 y 6, 6 y 5 -> 2
- 12: 6 y 6 -> 1
Es decir, que en 15/36 combinaciones salen los números ganadores. Esa es la probabilidad de ganar al lanzar los dados.
Tras empezar el juego, existen 3 posibilidades:
- Ganar 2 veces seguidas: La probabilidad de ganar 2 veces seguidas es 5/12 * 5/12 = 25/144
- Perder 2 veces seguidas: La probabilidad de perder 2 veces seguidas es 7/12 * 7/12 = 49/144
- Ganar y perder o Perder y ganar: La probabilidad de ganar y perder o perder y ganar es 2 * 5/12 * 7/12 = 70/144
Lo que ocurre es que cuando se gana y pierde se vuelve otra vez al inicio. Es decir, que hasta que no se gana o pierde 2 veces seguidas no se acaba el juego.
La probabilidad de salir ganador será por lo tanto la probabilidad de ganar 2 veces seguidas + la probabilidad de quedar igual * probabilidad de salir ganador. Matemáticamente resulta:
\(P = \dfrac{25}{144} + \dfrac{70}{144} \cdot P \rightarrow P = \dfrac{25}{74}\)
Carrera matemática
Alberto C. M. h dado con la solución:
En primer lugar expresamos el enunciado en forma matemática con el álgebra. Llamando \(t_{X}\) al tiempo empleado por el corredor \(X\) para llegar a la meta y a \(v_{X}\) a la velocidad del corredor \(X\), tenemos las siguientes relaciones:
\(v_{A}\cdot t_{A} = 100\)
\(v_{B}\cdot t_{B} = 100\)
\(v_{C}\cdot t_{C} = 100\)
\(t_{A} \cdot v_{B} = 95\)
\(t_{B} \cdot v_{C} = 90\)
\(t_{A} \cdot v_{C} = ?\)
Tenemos 5 ecuaciones para 3 incógnitas. Es decir, que de resolver el problema obteniendo todos los tiempos y velocidades, deberíamos de expresar las variables en función de una de ellas. Esto es lo que ha hecho Alberto, dejar la velocidad del A como variable independiente y expresar el resto de variables en función de ella y luego tomar cualquier valor. No obstante, en este caso nos piden obtener el valor de un producto, por lo que el parámetro independiente desaparece.
Obtendremos el valor de \(t_{A}\) y \(v_{C}\) usando \(t_{B}\) y \(v_{B}\) como intermediarios:
\(t_{A} = \dfrac{95}{v_{B}}\) \(v_{C} = \dfrac{90}{t_{B}}\)El producto resulta:
\(t_{A} \cdot v_{C} = \dfrac{95 \cdot 90}{v_{B} \cdot t_{B}} = \dfrac{8550}{100} = 85.5\)
Es decir, que el corredor \(C\) habrá recorrido \(85.5\) metros cuando el \(A\) llegó a la meta. Por lo tanto la distancia de separación es \(14.5\) metros.
Suma y resta cuadrática
MGL ha dado con la solución:
Tomando la primera pareja de números podemos expresarla como:
\(100^{2} – 99^{2} = (100+99) \cdot (100-99) = 100 + 99\)
Lo mismo ocurre para el resto de parejas, simplificando el sumatorio a uno más sencillo:
\(100 + 99 + 98 + 97 + … + 3 + 2 + 1\)
Que, a pesar de ser más sencillo, sigue sin ser trivial. El truco para poder calcular manualmente el sumatorio es agrupar las sumas: \(100 + (99+1) + (98+2) + … + (52 + 48) + (51 + 49) + 50\)
O, lo que es lo mismo:
\(100 \cdot 50 + 50 = 5050\)





Pista del primer acertijo: Factoriza los números y date cuenta de que los productos de los grupos deben ser los mismos
3=3
4=2^2
5=5
6=2*3
7=7
8=2^3
28=(2^2)*7
30=2*3*5
35=5*7
4*7*30=(2^2)*7*2*3*5=(2^3)*3*5*7=840
5*6*28=5*2*3*(2^2)*7=(2^3)*3*5*7=840
3*8*35=3*(2^3)*5*7=(2^3)*3*5*7=840
Es correcto Carlos! Gracias por tu respuesta! Intenta resolver el resto jejeje
Pista del segundo acertijo: En primer lugar obtén las probabilidades de ganar en la tirada teniendo en cuenta la probabilidad de sacar cada uno de los números ya que es diferente entre sí (por ejemplo, para sacar un 2 debe ser 1-1 pero para sacar un 3 puedes tener 1-2 o 2-1, es decir, el doble de probable sacar un 3 que un 2).
Una vez calculadas las probabilidades, es cuestión de jugar con ellas y darte cuenta de la recursividad.
Como son 2 dados de 6 caras, hay un total de 36 combinaciones. En 15 de ellas se suma 7, 8 o 9. Es decir que la probabilidad de ganar en la primera tirada es 15/36 = 5/12.
La probabilidad de ganar 2 veces seguidas es 5/12 * 5/12 = 25/144
La probabilidad de ganar y perder o perder y ganar es 2 * 5/12 * 7/12 = 70/144
La probabilidad de ganar es P = 25/144 + 70/144*P -> P=25/74
Correcto!!!
Pista del tercer acertijo: En primer lugar nombra cada uno de los segmentos y luego trata de encontrar una relación algebraica entre ellos teniendo en cuenta los triángulos rectángulos.
Pista del cuarto acertijo: Plantea las ecuaciones y ten en cuenta que la respuesta no es 15.
Si el A corre a velocidad V, el B corre a velocidad 95V/100 = 19V/20.
Como el C corre a 90/100 = 9/10 la velocidad del B, eso es que el C corre a velocidad 171V/200.
Si el A corre por ejemplo a 1m/s y tarda 100s, el C corre a 171/200 m/s, que multiplicado por 100s sale 171/2 = 85.5 metros. Entonces les separa una distancia de 14.5 metros
Correcto!! A ver si sacas otras
Pista del quinto acertijo: Piensa que debes encontrar una ecuación para relacionar el primer número de la secuencia con las sumas, teniendo en cuenta que lo difícil es saber expresar matemáticamente que el resto de números es suma del primer número y expresar de alguna manera los dígitos del resultado.
EDIT: NO ESTÁ RESUELTO AÚN EL QUINTO ACERTIJO. LOS COMENTARIOS RESPONDIENDO A ESTE SE REFIEREN AL SÉPTIMO ACERTIJO.
Espero haber acertado… Para el quinto problema, si el mayor número de la serie es n, el resultado de la suma ‘bonita’ es: (n^2 + n)/2 = 5050 en el caso de n=100. Curiosamente, coincide para cualquier n con el sumatorio de todos los números desde 1 hasta n. O sea, que 100+99+98+….+2+1 = 5050 también!
Hola Rubén, efectivamente la solución es 5050. Lo que estoy asombrado es de dónde has sacado esa fórmula jajajjajaja. ¿La has deducido tú o es la fórmula de una serie conocida? Lo que se pide es intentar juntar los números y los cuadrados para llegar a la solución asequible que has puesto de 1+2+3…+99+100 (que de por sí no es asequible, pero con una segunda reducción se hace muy fácil). ¿Eres capaz? ¡Inténtalo!
Se me ocurrió agrupar pares así:
100 x 100 – 99 x 99 = 100 + 100 x 99 – 99 x 99 = 100 +99(100-99) = 100 +99
98 x 98 – 97 x 97 = 98 + 98 x 97 – 97 x 97 = 98 + 97 (98 – 97) = 98 + 97
…
2 x 2 – 1 x 1 = 2 + 2 x 1 – 1 x 1 = 2 + 1 ( 2-1) = 2 + 1
De modo que el resultado es la suma de los primeros 100 números
O séa 5050 cómo dice la clásica fórmula
BINGO!!!!!!!!!!!! Es exactamente la solución buscada, gracias!!!!!!!!!!
Pista del sexto acertijo: No intentes usar matemáticas para obtener la solución puesto que necesitarás una simulación para obtener el resultado. Hay una forma lógica de encontrar la solución sin resolver ninguna ecuación.
Pista del séptimo acertijo: Intenta agrupar operaciones consecutivas y trata de encontrar una relación entre cada “pareja” para automáticamente aplicarla al resto y obtener el resultado.
Resuelto por MGL 🙂